Artículo ampliado el 17/02/23
Artículo siguiente: el metro como unidad del alma humana
A veces en matemáticas hablamos de números especiales por presentar unas propiedades muy particulares, así el 0 o 1, como unidad; o los números primos, los triangulares o los de Fibonacci.
Entonces Ramanujan le contestó: “No diga usted eso. El número 1729 es muy especial, pues es el número más pequeño expresable como suma de dos cubos de dos maneras diferentes, ya que 1729 = 13 + 123 y también 1729 = 93 + 103. ” Y de tal forma surgieron los números taxicab.
Es relativamente fácil tomar un número cualquiera y encontrar un montón de relaciones curiosas y, a veces, sorprendentes. Pero hacer esto mismo con el 377 parece ser asombroso.
El 377 es el nº 14 de la serie de fibonacci; de modo que 377 = 144+233, siendo como es sabido el 144= 12 x 12.
Lo curioso de este número compuesto, pues 377=13·29, es que parece tener una relación especial precisamente con el número 12, y sus múltiplos.
Esto me ha sorprendido al verlo, pero la verdad, siguiendo la serie de Fibonacci a través de su ecuación se aprecia lo fácil de establecer la siguiente serie de aproximación a 1:
A primera vista parece un sistema completamente antropométrico sin ninguna peculiaridad matemática, dado que codo, palmo y dedo parecen hacer referencia a partes del cuerpo humano. He visto algún trabajo interesante defendiéndolo y trabajando sobre tal suposición. Ciertamente, tomando los nombres como evidencias parece tener fundamento, aunque para que alguien tenga un "codo" de 0,5236 metros debe medir más de 1,90 metros.
1) Tomamos un circulo de diámetro 1 metro, de modo que su perímetro será Pi metros
2) Dividimos este perímetro en 6 partes iguales
3) Cada una de estas partes, entonces, mide 1 codo egipcio.
Por lo tanto, hemos creado un círculo de perímetro Pi y lo hemos dividido en 6 partes, de donde sacamos geométricamente el valor del codo real. Pero esto no es todo:
Si una parte del circulo es 1 codo, entonces el resto (las otras 5 partes del perímetro) nos muestran, de nuevo, una relación áurea:
Tenemos la gran pirámide de Giza, cuyo lado de la base mide 440 codos y la altura 280 codos. Me he dado cuenta que esto lo podemos expresar tal que así:
La cuestión es, pues, ¿y si los franceses revolucionarios, con Talleyrand en cabeza, conocían ya de antemano esta unidad secreta fundamental egipcia y simplemente la bautizaron con el nombre de "metro", sacándola a la luz para goce de la humanidad entera? Sería una acción, en verdad, muy típica de la ilustración y sus ideales.
Ciertamente la relación entre los revolucionarios franceses y el mundo egipcio es íntima y muy desconocida. Por ejemplo, ¿a qué vino esa expedición militar-filantrópica de Napoleón a Egipto?
Estamos ante una precisión en la velocidad de la luz que no se pudo superar hasta 1952. No significa eso que los egipcios tuvieran una idea técnica de la luz y la supieran dominar como llevamos haciéndolo desde hace 350 años. Pero nos abre la puerta a pensar que la velocidad de la luz se puede expresar de forma aproximada mediante Pi.
Sorprende ver como mediante el 377 obtenemos una expresión muy "limpia" de esta altura ideal. Sin embargo, no parece que podamos movernos mucho buscando relaciones.
En resumen:
A partir de medidas estrictamente egipcias es numéricamente factible ajustarlas a medidas métricas con las cuales el prototipo humano de 24 palmos adquiere un tipo de relaciones básicas que se pueden expresar de forma ya primal como pitagórica, al tiempo que definen la unidad métrica, es decir, el metro.
Artículo siguiente: el metro como unidad de medida del alma humana








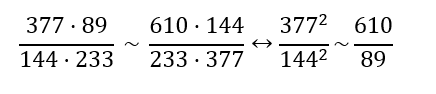



















No hay comentarios:
Publicar un comentario