Confieso mi fascinación por cuanto voy a exponer a continuación desde los 15-16 años, cuando en físicayquímica me puse a estudiar los 4 principios de la termodinámica.
No creo propiamente en las cosas, en los objetos, en las entidades, los hechos y los elementos ¡No me voy a flipar preguntándome de qué esta hecho el universo y cuáles son sus elementos constitutivos y esenciales! Pues tengo clarísimo que no hay tales cosas, sino devenir permanente.
En este sentido la noción de nada, opuesta a la de cosa, tampoco me preocupa nada. Y claro, no le hago mucho caso a la vieja pregunta metafísica: ¿por qué hay algo en vez de nada? Pues nunca hay realmente algo.
La "solidez", la "rigidez", la "permanencia", sensaciones harto primarias y rudimentarias sobre las cual hemos logrado imaginarnos un mundo de cosas fijas, estables, definibles y con entidad propia (idénticas a sí mismas con el tiempo), nos han permitido fantasear con la supuesta existencia de un mundo ontológico, formal, matemático y por tanto, lleno de objetos ¡Nos ha llevado a creer en un mundo metafísico! Y ciertamente este fantasear nos ha permitido adquirir un poder notable sobre la vida y, por tanto, el devenir. ¿Cómo negarlo?
El uso de mentiras y engaños, artificialidades y fantasías nos permite prosperar en la vida.
En esto soy nietzscheano, sí muy nietzscheano; aunque confesarlo conlleve que se burlen de mí. Y si bien me parece injusto, tampoco me indigna ni molesta; también yo me burlo muchas veces de ello, pues no pocas veces también me place ser injusto.
Así pues, la no-verdad, la ficción, la fantasía para nada me molesta, siempre y cuando nos favorezca: nos abra puertas, posibilidades y nos proporcione un cierto dominio y soberanía sobre la vida... la muy salvaje.
Uno siempre puede inventarse una idea nueva: la tomaremos por buena en la medida que nos sea fecunda y de su seno emerjan nuevas ideas y posibilidades que expandan nuestra comprensión. Y cuando tal fecundidad se agote y nos sepa ya caduca, entonces la cambiaremos por otra.
Nuestro conocimiento muda sus verdades como los árboles sus hojas, y así se perpetua.
No, no me molesta tomarme las cosas de muchas formas distintas, puesto que las cosas ni son de una determinada manera, ni tan siquiera existen realmente.
Panta rei.
Ay, que poco idealista soy: nunca me fijo en las cosas, en los hechos por sí mismos, en los elementos propiamente dichos, sino en las tendencias, en los procesos, en los desarrollos y las dinámicas. Pienso siempre en 4 dimensiones, por así decirlo. ¡Cómo no me va a entusiasmar la termodinámica si trata al mundo precisamente como puro procesar!
Pero asumo que la mayoría de la población alardea de gozar de un encefalograma plano: sólo ven las cosas que tienen delante de las narices, aquí y ahora ¡Sólo ven en dos dimensiones! En otras palabras, la mayoría de la población simplemente es idealista y dogmática. ¿Vivo en un mundo paralelo?
En definitiva, más que contar lo que sé sobre la termodinámica y compañía plasmaré lo que voy aprendiendo, mis reflexiones, dudas y posibilidades. Hay gente que tiene estos temas mucho más por mano que yo, hecho que tiene sus ventajas y desventajas.
Termodinámica: un relato sobre los procesos
Lo que siempre me ha fascinado de la termodinámica es que estudia procesos sin preocuparle si estos están hechos de átomos, moléculas, cosas, personas, eventos, estrellas, animales, objetos, espíritus, máquinas, o lo que sea ¡Se limita a estudiar evoluciones! Por tanto se trata de "la" teoría universal: se puede aplicar a cualquier tipo de proceso independientemente de la naturaleza bajo la cual se conciba.
En este sentido se puede considerar como el ABC de cualquier conocimiento que se precie de científico. Y sinceramente, de conocimientos científicos en este sentido hay menos de los que me gustaría. Por ejemplo, la historia, la sociología, la economía aún no lo han logrado en gran medida; aún tienden a estudiarse como una recopilación de datos y hechos que se entrelazan mediante relaciones causalistas muy discutibles y arbitrarias -ideológicas o personales las más de las veces.
La termodinámica se fundamenta sobre una única noción básica: energía.
¿Qué es la energía?
De algún modo es el poder de transformación o fluctuación que muestra lo estudiado. A más energía, más poder de fluctuar, modificar, transformar, vibrar, devenir muestra cuanto estudiamos.
Uno de los grandes logros de la física básica, pienso, ha consistido en desarrollar diferentes mecanismos para cuantificar este "poder de transformación".
Con el tiempo ha surgido, precisamente, la idea de que existirían distintos tipos de energía según como se iban midiendo; ahí tenemos desde la energía interna, la energía térmica, la energía electromagnética, la energía nuclear, etc...
De hecho, cuando los físicos afirman buscar los supuestos compuestos que conformarían el universo lo que buscan, si nos fijamos y prestamos atención, son mecanismos para medir cierta forma de energía: un tipo de transformación o fluxión ¡Y la cosifican!
Así, por ejemplo, la idea de electrón representa para el físico "algo" con energía, cuando más bien expresa una forma de medir cierta potencia de transformación y poco más; lo que ocurre es que nuestra mente siempre tiende a imaginarse cosas e hipostasiar ¡Si, nuestra imaginación tiene sus vicios!
La entropía
Una vez se definió la energía como la capacidad o el poder de transformación y evolución, la siguiente pregunta a realizar se presentó por sí sola: ¿Y qué trayectoria evolutiva adquirirá la energía? ¿Si la energía es transformación y cambio, hacia qué se transforma, hacia donde tiende, hacia donde se dirige el flujo?
Fueron los ingenieros, así Carnot o Clausius por ejemplo, al estudiar las máquinas de vapor durante la revolución industrial, los primeros en abordar el dilema de: "hacia donde evoluciona una cantidad de movimiento", "hacia donde va a discurrir un flujo", y, "hasta qué punto podemos controlar esta evolución".
Estos ingenieros se dieron cuenta de que jamás lograban máquinas capaces de generar trabajos con un 100% de rendimiento. Es decir, que les resultaba imposible forzar un flujo de energía para que discurriera completamente hacia un objetivo concreto.
Clausius directamente afirmó: es imposible que una máquina cualquiera emplee toda la energía recibida para hacer un trabajo concreto, pues siempre habrá energía que se "perderá" en el entorno, calentándolo ¡Todas las máquinas disipan energía!
Esta energía disipada, esta capacidad de transformación que "se nos escapa" descontrolada y que lleva a que lo estudiado nunca termine de evolucionar exactamente hacia donde nosotros queramos, se la llamó "entropía". Y los ingenieros la juzgaron como ingenieros: como energía inútil para el sistema ¡Simplemente porque para ellos era inútil por incontrolable!
Nada en la física me ha chirriado y contrariado nunca más que este juicio utilitarista e interesado que le adjudicaron los ingenieros a la entropía: que a ellos algo les parezca inútil no quiere decir que lo sea para el universo ¡Como si el mundo tuviera que plegarse a nuestros intereses y deseos, valoraciones y juicios por nuestra cara bonita!
Sin embargo, poco a poco la noción de entropía nos ha ido mostrando como el universo se nos muestra profundo, muy profundo; mucho más de lo que jamás hubiéramos podido imaginarnos.
¿Qué medimos cuando apelamos a la entropía?
A partir de los trabajos de Boltzmann la noción de entropía mudó: se cayó la idea de que todo proceso desgastaba la energía y que precisamente eso era la entropía: energía inútil.
Boltzmann redefinió la entropía de la siguiente manera: dada una energía o capacidad de transformación que conocemos midiendo la temperatura, el volumen, la presión, etc. podemos pensar que está constituida por "energías más pequeñas", es decir, por una multiplicidad de procesos menores que se pueden distribuir de muchas formas diferentes. Ahora bien, todas estas múltiples distribuciones diferentes son indistingibles entre sí, es decir, resultan equiprobables. Da lo mismo aquello que estudiemos tenga, en el fondo, una distribución concreta u otra ¡No le afecta para nada!
Entonces, la distribución de los subprocesos que constituye un proceso a estudiar puede ser harto variada y distinta; y sería una característica fundamental propia de la energía. Boltzmann, pues, también muda la noción de energía, volviéndola más compleja.
De alguna manera es como si con Boltzmann la energía medible no fuera ya una sustancia bien definida y fija, plana y bien determinada, una simple etiqueta quiero decir, sino una variopinta distribución de microprocesos posibles y todos ellos equivalentes entre sí ¡Por indistingibles para el propio sistema! De modo que no importa cual de ellos constituye realmente al proceso a estudiar. Simplemente se destaca que el proceso los percibe, a todos ellos, como idénticos y por tanto, equiprobables. Y como veremos, ello me parece fundamental al abrir de par en par las puestas al azar.
Con lo dicho, la entropía de un proceso a estudiar pasa a definirse como la distribución de microprocesos indistingibles que admite tal proceso. Cuanto mayor sea el número de microprocesos admisibles indistingibles, y por ello equiprobables, mayor será la entropía del proceso.
Véase como aquí ya no se habla de energía inútil y cosas dogmáticas por el estilo, sino que se "habla" de la cantidad de microprocesos admisibles, por indistingibles para el propio proceso a estudiar.
Indudablemente esta idea afecta directamente al tipo de evoluciones que manifestará el proceso, puesto que nos lleva de lleno a la teoría del caos. Pero dejemos esto por el momento.
De la teoría de la información
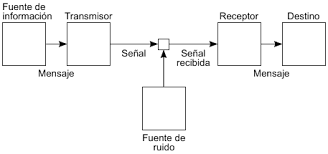
Claude Shannon, a mediados del s.XX, desarrolló la teoría matemática de la comunicación al estudiar los procesos de transmisión de datos. Partió de un esquema comunicativo simple tipo:
Emisor, mensaje, transmisor, canal, señal, fuente de ruido, receptor, destino.
Una persona (emisor) dice algo (mensaje) por su móvil (transmisor), que está conectado a internet mediante wifi (canal). El móvil convierte lo que dice esa persona en impulsos eléctricos (señal), que pasan por el wifi hasta otro móvil (receptor), que los traduce de nuevo a palabras para que lo escuche otra persona (destino).
Shannon, ingeniero de telecomunicaciones, intentaba controlar las fuentes de ruido de las comunicaciones.
¿Qué son las fuentes de ruido? Cuando un emisor lanza un mensaje y este es transformado en una señal por un transmisor para que pueda desplazarse mediante un canal y que un receptor pueda descifrar y recomponer el mensaje original, entonces siempre se produce ruido: fallos, pérdidas y errores de comunicación. Desde pequeños todos hemos jugado al teléfono y sabemos lo que ocurre ¡Eso se debe al ruido en las transmisiones!
Shannon, como ingeniero, tenía claro que para controlar el ruido en una transmisión tenía que poder medir y controlar, antes de nada, el mensaje. Y para poder medir un mensaje tenía que crear una unidad. Al trabajar con máquinas de comunicación lo más fácil era tomar el bit, o unidad booleana, como unidad de medida. Pues desde el telégrafo, a mediados del s.XIX, se sabía que todo mensaje se podría transcribir mediante el algebra de Boole. Y en efecto, hoy ya transmitimos cualquier mensaje, sea voz, visual, lectura, etc empleando sólo 0 y 1; pues mediante 0 y 1 podemos interactuar sin problemas con los transistores de nuestras máquinas eléctricas de comunicación (ordenadores, móviles, etc).
La idea fue, pues, que cualquier mensaje se puede medir mediante bits. Y a la medida de un mensaje se le llama "información". Cuantos más bits mida un mensaje más pesará, es decir, mayor será su tamaño ¡Contendrá más información!
Definido esto Shannon se dio cuenta de que todo mensaje contiene dos tipos de información:
-Una información inteligente formada por patrones, repeticiones, similitudes o simetrías. Es una información, por tanto, fácil de ser resumida, comprimida y simplificada. La llamó información redundante.
-Una información aleatoria, sin repeticiones, ni patrones, con lo cual resulta ser incomprensible, irreducible e insimplificable. La llamó ruido.
Se dio cuenta de que cualquier mensaje humano contiene ambos tipos de información y, además, que se pueden medir. Gracias a ello se volvía posible detectar las fuentes de ruido que van apareciendo en una transmisión de comunicación, dificultando la comprensión de los mensajes, y valorar hasta qué punto es posible eliminar semejante ruido.
Pero además, este trabajo permitió entender que todo mensaje con cierta inteligencia para nosotros siempre puede disminuir su información ¡Siempre es posible reducir el peso de un mensaje que contenga mucha información inteligente! De esta idea han surgido todos los programas de compresión de datos.
Shannon, junto con otros matemáticos, al final lograron alcanzar una forma, no sólo para medir la información de un mensaje, sino para medir hasta qué punto es comprimible un mensaje hasta dejarlo como puro ruido. Esta medida de la compresión de un mensaje es, precisamente, la entropía de un mensaje.
Así, pues, a mayor entropía y por tanto información aleatoria, que tenga un mensaje indica que mayor es su ruido. ¿Qué significa eso? Que mayor son el número de configuraciones de bits equivalentes que puede adquirir. Por ejemplo un mensaje que sea sólo un {0} (un bit en estado definido 0) casi no tiene ruido, al ser carecer de muy poca información ¡Sólo tiene un bit! Si al cero le añadimos un 1 y obtenemos un mensaje tipo {01} , entonces aumenta su información, su ruido y su entropía, que pasa a ser 2 bit.
Otro ejemplo:
si tenemos un mensaje a={01010101010101010101} y un mensaje b={11101011000011111000} de 20 bits cada uno, en un principio, vemos que el mensaje a es fácilmente comprimible (repite 10 veces {01}) al seguir un patrón muy evidente, mientras el mensaje b no lo es. De modo que la entropía del mensaje a será menor que la del mensaje b. Es decir, en una transmisión se requiere de más computación para adivinar el mensaje b que el mensaje a.
Tenemos, por tanto, que la entropía mide el ruido, la información irreducible, lo complicado de descifrar un mensaje porque son muchas las posibilidades que admite. Es decir, cuantos más estados equivalentes o indistingibles admita un mensaje, o proceso, más difícil será descifrarlo, al presentar más ambigüedades; y cuanto más difícil es descifrar un mensaje más fácil es que no lo logremos y terminemos obteniendo una transmisión caótica e impredecible.
Y todo lo contrario, cuando un mensaje presenta muchas redundancias, muchos patrones repetidos y por tanto fáciles de deducir unos a partir de otros, entonces el mensaje admite muy pocas posibilidades ¡Es un mensaje muy concreto y preciso! Con lo cual se puede comprimir y reducir a muy poco información, De modo que resulta más fácil que el destinatario obtenga una transmisión clara, determinada y exacta.
Complejidad
Tratando estos temas aparece de forma natural una nueva noción: la de complejidad.
De ordinario se define como complejo aquello que presenta un elevado números de partes, elementos, unidades las cuales, sin embargo, se encuentran interrelacionadas de alguna forma comprensible.
En tal sentido, lo complejo es aquello que si bien a simple vista puede parece complicado, embrollado y aleatorio es posible comprimirlo de algún modo. En otras palabras, aparece la complejidad en un mensaje cuando existe un algoritmo capaz de comprimirlo; y cuanto más lo comprima mayor será la complejidad manifiesta por el mensaje.
Por tanto, cualquier mensaje cuya entropía sea menor que su información es un mensaje susceptible de mostrar cierto grado de complejidad y por tanto, de ser reducido y comprimido.
En efecto, podríamos definir la complejidad como la cantidad de información redundante de un proceso, mientras que la complicación sería su cantidad de ruido.
Hablar de ello me ha recordado lo ya escrito sobre Chaitín y su número, y con él la definición matemática de aleatoriedad:
"En matemáticas, la teoría de la probabilidad o de la estadística estudia la aleatoriedad o el azar que es un fenómeno que ocurre cuando existe una serie numérica que no puede obtenerse mediante un algoritmo más corto que la serie misma." Del wikipedia.
Se entiende, pues, que en matemáticas se define el azar, precisamente, como una mensaje para el cual no existe manera alguna (ningún algoritmo, instrucción u operación) capaz de comprimirlo ni una sola pizca; con lo cual estamos ante puro ruido: una información 100% complicada de adivinar, con lo cual ahí es preciso "calcular" cada bit del mensaje para conocerlo, dado que resulta imposible deducirlo a partir de los anteriores por su ambigüedad.
Vale recordar, llegados hasta aquí, que esto nos lleva directos, entre otras cosas, a los números irracionales, como raíz de 2 o Pi. Son números cuyas cifras se suponen aleatorias con lo cual su aparición sería 100% complicada de hallar ¡Sería puro ruido! Hecho que da qué pensar.
Con la entropía el sueño racionalista se desvanece.
En el post anterior, sobre el Timeo de Platón, vimos como según el griego el mundo partía de una disposición pasiva y receptiva, es decir, de un grado extremo de entropía e información para ir generando formas vivas a partir de la fecundación del demiurgo
¡El demiurgo se muestra como una maquina de reducir entropía empleando un algoritmo divino (las formas ideales)!
Este proceso de fecundación terminaba, dice Platón, con la creación completa del universo como un ser animado perfecto y bello, eterno y bueno. En otras palabras, el demiurgo es capaz de reducir el ruido inicial a cero y con ello, mostrar un mundo completamente coherente, lleno de significado y por tanto, de una complejidad extrema.
También Leibniz trató a fondo esta cuestión: ¿acaso el mundo posee una complejidad infinita gracias a la acción divina, paradigma de todos los algoritmos posibles? Sin embargo a nosotros esta complejidad infinita siempre se nos aparecerá sumamente complicada; como puro ruido. Spinoza defendió algo parejo, y Einstein también cuando confesó buscar una ecuación definitiva de una pulgada capaz de explicarlo todo.
Sin embargo, con el tiempo hemos descubierto que la información que nos resulta una poco explicativa y significativa siempre mostrará un límite de comprensión y por consiguiente, también lo manifestará su complejidad. Es decir, que resulta imposible eliminar por completo cierto grado de ruido en una información.
Visto así, la teoría de la información me parece otra forma de demostrar lo mismo que demuestran los teoremas de incompletitud de Gödel: que dado un lenguaje suficientemente explicativo resulta imposible hallar todas sus verdades de forma deductiva.
En definitiva, Kant tenía mucha razón al criticar la razón pura, aunque su ciencia transcendental fuera un despropósito filosófico sideral. Pues resulta imposible deducir toda las verdades del mundo a partir de una verdad simple y fundamental. De modo que para desarrollar la ciencia, el poder de la deducción termina siendo muy limitado, con lo cual nos resulta imprescindible especular. ¿Especular? Sí, tirar de lo que Kant llamó "juicios sintéticos a priori", y gracias a los cuales podemos elaborar "verdades emergentes" -indeducibles directamente de sus axiomas pero permitidas por éstos.
La ley de Weber
Hace ya un tiempo expliqué, muy por encima como siempre hago, en qué consistía esta ley; una ley psicofísica estipulada a principios del s.XIX.
También comenté su importancia en un montón de ámbitos, dado que habla sobre la percepción y en concreto, sobre los umbrales de percepción, los cuales regulan nuestra configuración de la realidad y por tanto, afectan directamente a nuestra toma de decisiones, nuestro comportamiento, incluso nuestros valores ¡De cómo nos valoramos a nosotros mismos dentro de un sistema!
Sin embargo, esta ley psicofísica no sólo actúa sobre las personas, sino también sobre la naturaleza. De algún modo pone de manifiesto que los sistemas físicos "perciben" la realidad, su entorno; y según como lo perciban se comportan de una forma u otra ¡Incluso adquieren unos valores u otros!
Es cierto que la física clásica, la que defendía Einstein fruto de la teología y la metafísica moderna, consideraba que el mundo material se comportaba de forma determinada, exacta y sin ambigüedades al seguir una leyes precisas, necesarias y universales ¡Cómo un reloj suizo!
De algún modo se creía que todo sistema físico poseía unas propiedades innatas, propias, objetivas, y como tales no dependían de como los demás sistemas lo percibían, sino de ellos mismos. Y se defendía que era sobre tales propiedades objetivas que los sistemas actuaban y se comportaban de una forma determinada u otra con los demás sistemas, mostrando unos valores u otros.
Es cierto que con el advenimiento de la mecánica cuántica, a raíz del principio de incertidumbre de Heisenberg, y el cual lo podemos interpretar como un umbral de percepción, esta idea metafísica se rompió; al menos para el mundo microscópico.
Pero pienso que con lo que nos muestra la ley de weber esa vieja idea metafísica se puede romper también para el mundo macro. ¿Por qué? Porque los sistemas físicos no tienen valores objetivos. Por ejemplo, por sí misma una piedra no pesa 10 kg. Estipular el peso de una piedra es fruto de poner la piedra en cierto equilibrio con un peso de referencia. Y para poner dos "cosas" en equilibro es necesario buscar una manera en la que ambas se perciban como iguales. Hecho que para nada demuestra que sean iguales, sólo que se perciben como tales.
Esta cuestión ya la menciona Poincaré a vuelapluma en su "ciencia e hipótesis". Nos muestra como al intentar interpretar el mundo físico como un conjunto de medidas, y por tanto valores, siempre ocurre lo siguiente: que el principio de transitividad se rompe en algún momento crítico. Y esta violación lógica se interpretó como "error experimental", hecho que nos llevó a una carrera loca para mejorar continuamente nuestros instrumentos de medida.
Veamos brevemente esta violación lógica en las medidas:
Dado un sistema de medida, el cual en esencia consiste en crear un mecanismo que busca encontrar un punto de equilibrio (una igualdad) entre dos cosas, y numerar a través de una escala arbitraria este punto de equilibrio, siempre hallaremos 3 cosas, acaso llamadas A,B,C que rompen el principio de transitividad tal que así:
A = B
B = C
C < A
Al chocar con este absurdo siempre se ha dicho: -Es que hemos alcanzado el límite en la precisión del instrumento, con lo cual éste falla-. Pero, ¿es esto realmente un fallo y un error de medición?
Bueno, si pensamos de forma dogmática y aún creemos que las cosas poseen cualidades ocultas, objetivas e innatas, las cuales se pueden revelar mediante "la magia" de nuestros instrumentos de medida, pues será un error y un fallo, claramente. Pero hay otra forma de interpretarlo. Una forma mucho más mundana.
Por un lado podemos pensar que A y B se perciben como iguales dentro del sistema de medida diseñado. Que B y C también se perciben como iguales. Y sin embargo que A y C no se perciben como iguales, sino que dentro de tal sistema de medida concreto uno se percibe mayor que el otro, generando un claro desequilibrio.
Así pues, tenemos que B admite A y C como equipotentes y por tanto indistingibles ¡Aunque A y C se perciban entre sí como diferentes y discernibles! Y sí, lo podemos obviar como se lleva siglos obviándolo, pero la naturaleza parece siempre jugar con esta ambivalencia perceptiva que a simple vista nos parece loca e irracional.
En este sentido me da por imaginarme, y lo cuento de manera informal, que la entropía de B, su ruido característico según el instrumento de medida empleado, de algún modo puede entenderse como la capacidad de B de admitir sin problemas A,C, dado que los percibe iguales, es decir, equipotentes.
Sin embargo, cabe recordarlo de nuevo porqué aún se enseña así en las facultades de ingeniería: que esta violación lógica durante siglo nos llevó a esperar poder ir mejorando nuestros instrumentos de medida, reduciendo cada vez más el ruido en las mediciones, hasta sacar a relucir "el verdadero" valor innato de las propiedades medibles.
Sin embargo, con el principio de incertidumbre de Heisenberg se hace ya patente que no; pues sí existe un límite en la capacidad de reducir el ruido en las mediciones. Y que pensar "las cosas" como que poseen propiedades ocultas y objetivas, innatas y metafísicas, pues no deja de ser más que un recuerdo de nuestra superstición metafísica más antigua, sobre la cual nacieron y crecieron nuestras ciencias modernas.
En fin, una vez más chocamos con la misma idea de nuevo: el ruido aparece siempre en todo proceso y siempre existe un límite a partir del cual es imposible eliminarlo ya más: la entropía; que define la cantidad de microprocesos que admite lo estudiado porque los percibe como indistinguibles, equipotentes, iguales. Y para descifrar cuál es el microproceso que rige lo estudiado hay que operar.
¿Y qué significa operar?
Siempre me ha parecido curioso que Kant defendiera que la operación, el cómputo, la resolución fuera un juicio sintético a priori, es decir, fuera una actividad emergente. Es decir que el resultado de un cómputo nos dice siempre más que las partes que operan ¡O nos dice algo distinto de las partes!
De la compresión (deducción) al ruido (azar)
Venimos de una tradición idealista milenaria que veneraba la razón pura, es decir, la idea que a través de una primera verdad fundamental se podían deshilar sin problemas todas las verdades posibles y mostrarlas tal cual eran para goce de nuestra inteligencia más prístina e inmaculada.
Después de mucha lucha, fracasos y tentaciones hemos descubierto, aunque ya algunos como Kant, Schopenhauer o Nietzsche nos lo avisaron bajo distintas persuasiones, que este ideal racionalista no es viable ¡Nos lleva a un callejón sin salida! Con lo cual ya no podemos ver la vida como una máquina perfecta y buena, omnisciente y eterna. ¿Significa eso que la vida es una mierda, un juguete roto y desechable destinado a criar malvas?
No, no somos pesimistas.
De repente apreciamos como la muy salvaje ignora muchas cosas de sí misma, hecho que la pinta de un halo encantador, exótico e insondable, mientras nos la viste de bailarina.
Sí, poco a poco comenzamos a entender cómo del determinismo deductivo y racionalista más duro se pasa a una visión aleatoria, intuitiva y emergente de la vida. "Una pizca de razón siempre es posible, pero el mundo prefiere bailar sobre los dedos del azar" Nos susurra Zarathustra, y ya comenzamos a entenderlo.
Sin embargo, aún son muchos quienes de un modo u otro añoran el viejo sueño idealista y como burros persisten en adentrarse en lo inviable. Miradlos como suspiran con hallar la fórmula definitiva que les explique la vida hasta el detalle. Pobrecillos, necesitan de un manual para bailar con ella ¡Es de risa verlos tropezar después de tres pasos! Y encima los cabezotas le recriminan des del suelo: -no tenías que haber hecho eso- Pero ella sigue bailando.








No hay comentarios:
Publicar un comentario