Confieso que me fascina tan singular y raro tema. Y mi opinión ha ido evolucionando un poco estos meses, aunque siguiendo una línea más o menos marcada.
A cualquiera le sonará ridícula semejante pregunta, dado que los números son lo que desde pequeños nos enseñan al contar; así el 1,2,3 o 4 por ejemplo.
Tenemos los números tan asumidos, integrados e interiorizados que ya no los "vemos" ni entendemos; como tampoco nos vemos a nosotros mismos sin que alguien nos acerque un espejo.
Pero la noción de número es un problema si nos atrevemos a tomarnos la molestia de observarlos de nuevo como si fuera la primera vez. A fin de cuentas, estamos ante una idea que costó milenios construirla, aceptarla, para luego interiorizarla poco a poco hasta esperar a que empezara a germinar y dar sus primeras flores.
Según los griegos más antiguos, por ejemplo, los números se concibieron simplemente como relaciones proporcionales harmoniosas, es decir, "razones". Es una idea que surge directamente de esa extraña y maravillosa noción presocrática que Aristóteles llamó "arkhé" y Tales de Mileto introdujo en Grecia. Ésta dice: todo, aunque parezca diferente, variado, multiforme e, incluso, contradictorio, esconde un denominador común, una unidad común, es decir, un mismo origen o razón de ser
A partir de la edad moderna, con la introducción y estandarización de un alfabeto específico para expresar las relaciones proporcionales, la noción de número fue tomando cuerpo e identidad propia dentro de la psique del sabio occidental, cuya mente empezó a pensar de forma inconsciente e involuntaria: si escribo "1" es porque debe de existir algo concreto y preciso al que atribuirle dicha noción. Y puesto que en geometría ya se había concebido el punto como lo más concreto y preciso, ya para el s.XIX se concebían los números, no como cantidades, sino directamente como puntos imaginarios ordenados de menores a mayores.
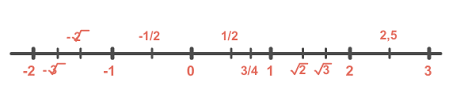
Por similitud a los puntos, pues, se pensó: dado que lo puntos se agrupan y ordenan geométricamente formando rectas imaginarias así mismo sucedería con los números: que se agrupan en una recta numérica imaginaria: la recta real.
De hecho, cuando esos sabios modernos se imaginaban una recta cualquiera ya fantaseaban con ver allí sólo números ordenados dando valor a sus puntos constitutivos, pues el algebra moderno abierto por Descartes permitía imaginarse este tipo de escenarios sin dificultad.
Demócrito con sus "indivisibles" se enorgullecida de haber sido el mejor matemático griego al ser el primero en solucionar el dilema de la división infinita ya planteada por Pitágoras por un lado y luego por Parménides y Zenón por otro. Pero contra Demócrito se levantó con suma indignación Platón y todos los matemáticos platónicos: desde Eudoxo hasta Arquímides.
Ya en "nuestra época", han sido Cantor y Dedekind quienes han justificado que sí, que los números atómicos, indivisibles y por ello irracionales existen y se "intercalan" entre los números infinitamente divisibles. Pero tal idea ha sido puesta en duda por gente como Chaitin; al menos se duda de que los irracionales se encuentren en la recta de los reales intercalados entre los divisibles.
Los números irreducibles o no-unitarios.Quizás, con la noción de número nos topamos, básicamente, con un problema de representación, el cual nos lleva a problemas de comprensión. Al final, concebimos los números según los representamos y en base a ello, así los tratamos.
Para empezar, cabe observar que el primer problema de representación nos llega ya con los números racionales con infinitos decimales, así el 1/3 por ejemplo, que parecen irrepresentables como puntos de una recta, en el sentido de que no tienen una representación unitaria concreta en decimales:
1/3= 0,3333333... ¡Resulta imposible partir una "unidad de longitud" en 3 segmentos exactos!
Con razón a estas fracciones les debemos la primera paradoja aritmética:
3x0,333333333...= 0.999999... pero dado que 3x(1/3)= 3/3=1, entonces la duda es: ¿Cuál de los dos resultados va a ser cierto?
No es difícil de justificar, sin embargo, que 1 = 0,9999999... utilizando las peculiaridades especiales del infinito. Eh aquí una demostración ejemplo típica y que se encuentra en la wikipedia:
Lo que ocurre es que tampoco es difícil justificar que 1 > 0,9999...
1 = (9 + 1)/10 es lo mismo que 10 - 9 = 1
1 = (99+1)/100 es lo mismo que 100 - 99 = 1
1 = (999+1)/1000 es lo mismo que 1000 - 999 = 1
1 = (9999+1)/10000 es lo mismo que 10000 - 9999 = 1
Y si llevamos esto al infinito entonces tenemos que:
100....0 - 99999...9 = 1
Resulta fácil aceptar, visto así, que 1 > 0.99999. De hecho, y como ya se ha comentado tantas veces en este blog, Cantor suele tratar el infinito de este modo, es decir, intentando respetar el finitismo a través de esa exigencia interpretativa que impuso Hilbert a principios del s.XX, y que decía algo así: el infinito debe ser un reflejo fiel de lo finito. Por lo tanto, lo que aquí sorprende, una vez más, es apreciar como según qué tratamiento escojamos para operar con lo infinito, obtenemos dos posibles resultados de la igualdad.
En cualquier caso, queda patente con la primera forma de tratar la igualdad, es decir cuando apreciamos (1/3)x3= 0.999...=1 que empleando la magia de los límites al infinito resulta factible pasar sin problemas de números inmedibles y con decimales sin fin, a números concretos y relativos a la unidad. Es como si pudiéramos utilizar dos tipos de representaciones equivalentes: una de unitaria (1) y otra de no unitaria (0.999...). Curioso.
Salta también a la vista otro aspecto: si bien mucho se habla de los irracionales el problema de la irracionalidad e inconmensurabilidad empieza ya con estas fracciones irreducibles a la unidad, dado que exigen que dividamos dos números que no se pueden dividir por ser coprimos.
1/3 nunca será divisible de forma exacta
Hecho que, curiosamente, no preocupó a los antiguos, al menos a los pitagóricos. Ya en seguida consideraron que este tipo de inexactitud se podía solventar, simplemente, cambiando el valor de la unidad, es decir, escogiendo de forma convenida el sistema de unidades.
Y en efecto, si se toma por unidad un número supercompuesto, como sería el antiguo y fascinante sistema sexagesimal Sumerio (unidad=60), entonces muchas fracciones irreducibles en el sistema decimal devienen reducibles a la unidad sin problemas, dado que en el decimal la unidad representa el 10, y por tanto es un compuesto con sólo 2 factores: el 2 y el 5.
Así pues por ejemplo, 1/3 es reducible a la unidad sexagesimal y puede representarse como 0,20.
En sexagesimal 1/3 es una división exacta
Con razón, por ejemplo, Platón parece venerar el factorial de 7 (7!=5040) como unidad de media, al tratarse de un supercompuesto: tomando el 7! como unidad de medida social Platón, en la República, explica cómo es posible generar muchas particiones, grupos y subgrupos de forma exacta para el buen funcionamiento de la ciudad, tanto en tiempos de paz como de guerra (aquí un trabajo al respecto). ¡Y qué decir de Ramanujan y su pasión por estos extraños y escasos números, los supercompuestos (ver aquí un brillante artículo al respecto).
Los números irracionales
Pero después de estos racionales irreducibles llegaron las raíces, como raíz cuadrada de 2 o el número áureo. Se les colgó el nombre de irracionales porque no surgen de la división de un segmento unitario.
En efecto, las raíces no son fruto de dividir segmentos unitarios; no surgen de un fraccionamiento ni de la partición de una distancia entera ¡No surgen de dividir dos números naturales cualquiera! ¿De donde surgen pues?
Geométricamente las raíces surgen de partir figuras más complejas: la raíz cuadrada surge de dividir un cuadrado o rectángulo por la diagonal; la raíz cúbica de fragmentar un cubo en un conjunto de subcubos, etc. Y el número áureo de ir dividiendo un rectángulo siguiendo la serie de Fibonnacci.
Pero desde una representación algebraica surgen de una idea curiosa y sencilla:
-Para la raíz cuadrada de un número x: Dado un número x cualquiera, entonces, hay que encontrar 2 números iguales que multiplicados entre sí den x.
-Para la raíz cúbica de un número x: Dado un número xcualquiera, entonces, hay que encontrar 3 números iguales que multiplicados entre sí den x.
-Para la raíz a la cuarta de un número x: Dado un número x cualquiera, entonces, hay que encontrar 4 números iguales que multiplicados entre sí den x.
etc,etc, etc...
Nota breve:
Esta definición aritmética me ha dado pie a pensar en una demostración muy simple sobre la irracionalidad de la raíz cuadrada de x, siendo x un número natural cualquiera no cuadrado, porque podemos entender la raíz cuadrada como la división de x por un número que será idéntico al resultado:
raíz cuadrada (9) = 9/3 = 3
Y también se puede demostrar la irracionalidad de cualquier raíz cúbica de x, siendo x un número natural cualquiera no cúbico, porque podemos entender la raíz cúbica como la división de x por un número cuadrado m que da por resultado raíz cuadrada de m:
raíz cúbica (27) = 27/9 = 3
Y de este modo es fácil generalizar la demostración para cualquier tipo de raíz:
Así pues, queda demostrado que llamamos raíces a divisiones o fracciones ejercidas sobre objetos geométricos de 2 o más dimensiones.Representaciones de las raíces
Bien, vemos como las raíces no pueden expresarse como divisiones simples de una dimensión, es decir, como un simple corte de segmentos enteros y, con ello, de la recta real. Ahora bien, parece ser que ya los griegos entendieron que pueden representarse como fracciones continuas o iteradas hasta el infinito de distancias enteras. ¿Y qué es eso? Iteraciones continuadas de división o fragmentación de una distancia.
Un ejemplo de fracción continua para representar la raíz cuadrada de 2:
Representar cualquier raíz cuadrada como una fracción continua al infinito resulta harto fácil. A mí mismo no me costó nada el otro día encontrar lo que luego descubrí que ya había sido inventado por el matemático italiano del s.XVI Rafael Bombelli (ver
aquí). Y podemos resumirlo así de simple:
¡Pero más curioso aún! De algún modo Eudoxo, brillante discípulo de Platón, al trabajar la raíz(2) se dio cuenta de que su fracción continua podía representarse como una secuencia de fracciones concretas e irreducibles que cada vez se aproximaban, ya por la derecha ya por la izquierda, más y más a raíz(2). Con ello presentó lo que hoy conocemos como la escalera de Eudoxo:
Esta escalera pudiera parecer que preludia ya los trabajos de Dedekind, en la medida que nos presenta raíz(2) como un número que siempre estará intercalado entre dos fracciones, por más que vayamos acotando la distancia entre ellas hasta el infinito. Es decir:
En efecto, de algún modo Dedekind, con sus famosas cortaduras expone lo que se puede interpretar de esta escalera de fracciones intercaladas: que si lleváramos esta desigualdad al infinito, entonces, a la izquierda, tendríamos en progresión todas las infinitas fracciones menores que raíz(2), y a la derecha todas las infinitas mayores; siendo precisamente raíz(2) el punto atómico al infinito de estos dos conjuntos de fracciones.
A partir de esta idea, y los posteriores trabajos de Cantor, los matemáticos pusieron sobre la mesa la hipótesis del continuo; que dice: ¿realmente la recta real está llena de puntos, o habría vacíos?
La recta real y el continuo
Con las cortaduras de Dedekind parecía demostrarse que la recta real está constituida íntegramente por puntos/números ordenados de forma inmediatamente consecutiva uno tras otro: cada cortadura sería un punto de la recta, y cada punto un número -los racionales serían números concretos, mientras los irracionales, como raíz(2), serían números que andan escondidos entre los racionales y que sólo podemos alcanzar la llevar los racionales al infinito. Así pues, con las cortaduras de Dedekind se justifica que la recta real sea continua.
Ahora bien, llegó Cantor, que interpretaba el infinito ya no como un límite, sino como un alcanzar un estadio final que reflejaría todo lo finito. Bajo esta manera de interpretar el infinito desarrolló, primero, su famoso teorema para determinar el tamaño de todos los conjuntos potencia, incluso el de los conjuntos infinitos. Y ante el curioso resultado obtenido se puso a comparar los tamaños de distintos conjuntos infinitos, justificando con su método que el conjunto de los infinitos racionales era de un tamaño inferior que el conjunto de los infinitos irracionales. A partir de aquí Cantor construyó una jerarquía de infinitos infinitos.
En efecto, Cantor justificó que si bien habría infinitos números irracionales e infinitos números racionales, el conjunto de los infinitos irracionales ha de ser de un grado mayor que el de los racionales; que serían infinitos en grado 0. En otras palabras, Cantor presenta la existencia de infinitos con distintos tamaños, unos con un grado de infinitud mayor que otros, y donde el conjunto de los números racionales representarían el grado básico, o cero, de infinitud; mientras el conjunto de los irracionales, en principio, representaría el grado 1 de infinitud ¡Siempre y cuando la recta real fuera continua!
Esta es la hipótesis del continuo: si existiera un conjunto infinito de números distintos a los racionales y a los irracionales que fuera mayor que los racionales pero menor que los irracionales, entonces, los infinitos irracionales pasarían a ser de grado 2, por decirlo de forma fácil, y ello conllevaría que la recta real no sería continua: contendría espacios vacíos.
En cierta forma, pues, Cantor pone en duda el trabajo de Dedekind, que dejaba claro que la recta real era continua y sólo estaría formada por racionales en lo concreto; y por irracionales al infinito. Y, ¿por qué lo pone en duda? Porque Cantor trabaja bajo la ilusión de una idea del infinito muy peculiar. Una idea que haría revolver de sus tumbas a Platón, Eudoxo, Euclides o Arquímides, pero que fascinó a los matemáticos del s.XX y XXI.
Esbozo breve sobre lo infinito
No hay nada más antigriego que ese idealismo germánico del s.XIX promocionado por Hegel y que conquistó parte de la Europa moderna, según el cual se podría trascender lo finito a caballo del infinito hasta alcanzar las entidades metafísicas: acaso los números en sí mismos como puntos o entidades atomizadas y aisladas de todo.
Es cierto, que siendo joven Platón nos presentó por primera vez la metafísica con su mundo de las ideas como entidades en sí mismas que se encontraban tan lejos de nuestra mundanidad concreta, relativizada y limitada por multitud de circunstancias, que resultaban inalcanzables sin la ayuda la la "manía" divina. Sin embargo, en sus diálogos eminentemente más matemáticos y maduros, como el Parménides, el Sofista, el Teeteto o el Timeo, Platón parece replantear de raíz esa primera dialéctica trascendental, tachándola de ignorancia juvenil.
Ahora bien, la evidencia más fuerte que nos lleva a pensar que Platón dejó de creer por completo en la trascendencia quizás nos la encontremos al analizar las ideas matemáticas de sus discípulos, Eudoxo y Euclides, ¡por no decir Aristóteles!, quienes, ya niegan sin tapujos que el infinito sea un salto trascendental al vacío sideral: al mundo de las cosas en sí. No, el infinito no sería un salto que nos permitiese ir de lo particular a lo universal, de lo aparente a lo esencial, de lo imperfecto a lo perfecto, de lo condicionado a lo incondicionado y libre ¡Y mucho menos sería una cantidad!
¿Fue el propio Platón quien descubrió otra forma de entender lo infinito o acaso la aprendió de otros y, entonces, la usó para replantear todo su pensamiento? Es difícil saberlo, pero a partir de Platón y sus trabajos de madurez, el infinito deja de concebirse como algo a alcanzar entre la inmensa mayoría de matemáticos griegos ¡Ya no se concibe como un estadio al que llegar mediante un salto inmortal definitivo!
A partir de ese momento, primera mitad del s IV ac, el infinito deviene, sencillamente, una forma de tratar las ideas ¡Un poder! El poder acercarte o alejarte de una idea tanto como se quiera; el poder crecer o empequeñecerse tanto como se quiera; el poder romper o recomponer una idea tantas veces como se quiera ¡Y nada más!
En definitiva, a criterio de los antiguos platónicos el infinito sería, en exclusivo, una potencialidad, jamás una realidad; como sí los parece ser para Cantor y Hilbert. Y no me escondo: me sorprende que se hayan tomado en serio los trabajos de Cantor sobre el infinito, dado que niegan la noción matemática de "límite al infinito" heredera directa, precisamente, de los antiguos al definirse como pura potencialidad: un poder acercarse a algo tanto como se quiera, y nada más.
Y me sorprende aún más cuando Cohen, a mediados del s.XX, dejó patente que la hipótesis del continuo resulta completamente trivial. ¿No pone eso ya de manifiesto que el propio trabajo de Cantor no nos dice nada esencial de las matemáticas y sólo presenta una interpretación entre otras posibles?
Mejorando la escalera de Eudoxo: la superfracción.
Honestamente, no quería extenderme tanto con este post, pero una cosa me ha llevado a la otra y, ahora mismo, me parece adecuado contar algo que me quería guardar un tiempo más. Así pues, lo dejo y ya está.
Es curioso como funciona la mente porque cuanto acabo de escribir viene a coalición de ciertos "juegos" matemáticos que llevo realizando estos días por mera curiosidad sin haberme preocupado por los intríngulis que acabo de escribir. Es decir, lo que voy a contar es fruto, sólo, de pasar el tiempo buscando distintas formas de representar un número cuadrado, para luego jugar a buscar formas distintas para resolver raíces. No había ninguna pretensión más que un pasatiempo. Y sólo ahora que he encontrado, sin más, algo quizás interesante me doy cuenta de todo lo que he apuntado a vuelapluma en este post.
Lo primero: tanteando distintas formas de resolver raíces he encontrado una escalera alternativa a la de Eudoxo para raíz(2). Vale decir que desconocía este trabajo del griego, hecho que me ha permitido entrar un poco más a fondo en su pensamiento al alertar que él ya había descubierto algo similar hace 2.500 años. Y sí, un tipo muy interesante el discípulo de Platón.
Mi escalera es esta:
Y si recordamos la de Eudoxo es la siguiente:
A simple vista parecen de algún modo inversas: los denominadores de mi escalera son los numeradores de la de Eudoxo. Y ambas "persiguen" el valor de raíz(2) mediante una aproximación alternada de valores.
Además, se observa como ambas escalas se pueden construir mediante una misma fracción algebraica generatriz; ésta:
Ahora bien, por lo que he podido leer no parece que Eudoxo, ni otros como Rafael Bombelli, que según parece también trató los trabajos de Eudoxo, hayan hecho ya mucho más al respecto. Pero me parece a mí que sí es posible hacer algo más. De hecho, parece posible hacer dos cosas más:
1) Generalizar esta fracción algebraica para todas las raíces cuadradas.
2)Encontrar una superfracción algebraica general capaz de definir todas las raíces cuadradas.
1: Para generalizar esta fracción algebraica sobre todas las raíces cuadradas simplemente hay que partir del método de Bombelli para generar fracciones continuas sobre raíces cuadradas y convertir cada paso en una fracción, tal que así:
2)Para hallar una superfracción general basta con desarrollar algebraicamente lo anterior de tal forma:
Pongamos 2 ejemplos tomando la superfacción a s = 7:
OBSERVACIONES:
Lo primero que salta a la vista es que definimos la raíz cuadrada de un número no cuadrado como el límite al infinito de la superfracción.
Ya hemos comentado como el límite al infinito matemático es una noción en esencia platónica y significa potencialidad. Con lo cual, el límite de la superfracción cuando "s" tiende a infinito significa que "s" puede crecer tanto como se quiera, de manera que resulta la mar de fácil pensar en modo platónico total y deducir, de ello, que la fracción puede dar valores tan próximos a raíz(2) como se quiera. Aunque, eso sí, el límite para nada significa que "s" tenga que llegar a un punto infinito donde la fracción adquiriría, entonces ya de golpe, un valor final metafísico y de por sí: el propio valor de raíz(2).
Excepto las mentas más lógicas, la mayoría suele interpretar el límite matemático a lo platónico. Pero quizás aquí sería interesante pensarlo de forma algo distinta; a saber: que al tender "s" a valores cada vez mayores el propio valor de raíz(2) se va haciendo más preciso ¡Va tomando cuerpo y creciendo! Pues, quizás, valga la pena presuponer que no preexiste un valor de raíz(2). Es decir, quizás sea interesante partir de una visión algo más constructivista o bien, operativista.
En los trabajos de Dedekind se aprecia sin dificultad como el alemán hace una interpretación matemática basada, estrictamente, en esta idea platónica de límite cuando apunta que un número irracional vendría a ser el límite al infinito de un conjunto de fracciones. En otras palabras, como platónico interpreta este límite como un aproximarse más y más hacia un punto concreto y con valor propio ya preexistente, al que llama cortadura. ¿Acaso no es eso vendernos como real algo que, matemáticamente hablando, sólo sería una pura potencialidad?
En cualquier caso, a nivel matemático definir los irracionales como límites al infinito de conjuntos de racionales parece ser perfectamente coherente y evidente con solo observar las fracciones continuas, la escalera de Eudoxo o la superfracción aquí presentada. En este sentido no habría ningún problema en concebirlos, ya no como puntos con un valor prefijado y concreto de antemano a los que aproximarse, sino como puras potencialidades.
Ir al límite
Cada cual lee y comprende las cosas a su manera. Las nociones matemáticas no son ninguna excepción, aunque haya un control férreo en intentar establecer consensos amplios, claros y firmes para definir sus conceptos de forma que sean aceptados para todos los matemáticos y así intentar evitar lo inevitable: que en las matemáticas surjan destellos arbitrarios y discutibles, dando la imponente sensación de mostrarnos la divina certeza que esconderían las cosas.
Lo reconozco, a mi parecer la visión de Cantor sobre los infinitos no me sabe mal. De hecho me resulta fascinante y quizás útil en ciertos ámbitos; por el ejemplo el computacional. Simplemente destaco que no es la única. Además, me extraña que se haya tomado en serio durante un siglo largo, como ya he comentado, cuando abandona impunemente la noción de límite en la interpretación que hace del infinito para, luego, interpretarlo empleando métodos finitistas; como por ejemplo la diagonalización.
En tal sentido, me parece que Cantor trata el infinito más bien como un lógico, es decir un mecánico del pensamiento, y no como un matemático, cuando nos lo presenta como si fuera una entidad coherente, precisa y bien estructurada; en vez de tomarlo como pura potencialidad.
En tal sentido, tratar "el límite al infinito" como pura potencialidad nos permite pensar y definir los "números irracionales", ya no como números reales, es decir, como supuestos puntos sutilísisimos escondidos en la recta real entre los racionales, sino como valores potencialmente emergentes de entre los racionales, los cuales a su vez serían valores potencialmente emergentes de entre los reducibles a la unidad, es decir, los números divisibles de forma exacta. Éstos, entonces, ya sí serían los únicos números reales por estar perfectamente definidos.
En fin, seguramente sea inevitable tener distintas formas de interpretar lo infinito, y aunque quizás la de límite sea de las más potentes no es la única posible, como muestra Cantor. Es más, quizás incluso serían posibles otras formas aún inauditas de interpretarlo, tal y como de algún modo parecen vislumbrarse entre algunos trabajos de Euler, Riemman o Ramanujan.
Crítica a los números
Acabamos de ver como Dedekind se basa en un prejuicio principal ya muy antiguo: que las raíces son números, que los números son puntos aislados y con valor propio, y por consiguiente deben de ser visualizados como átomos constitutivos de la recta imaginaria que se llama "real" y que mediante nuestras operaciones al límite podemos aproximarnos a ellos tanto como queramos.
A mí parecer, no estamos ante puntos ni tan siquiera ante valores prefijados; simplemente estamos ante puras operaciones. Operaciones que no nos han caído del cielo, sino que las hemos creado nosotros, perfeccionándolas, en la medida que nos han sido frutíferas y necesarias, inquietantes, incluso atractivas.
Entiendo que no somos conscientes de que, cuando decimos "raíz(2)", no estamos anunciando ningún número, sino dando una orden para llevar a cabo un tipo de operación muy concreta. Y en este caso, son operaciones de cierta complejidad que, para hallar un valor fijo, no podemos reducirlas a operaciones más simples como una suma o una resta ¡Ni tan siquiera la podemos reducir a una simple división irreducible equivalente! Este pensamiento me ha llevado a las siguiente reflexión:
Los números son definidos por operaciones, nunca por supuestos valores intrínsecos y esenciales.
Ya en algún otro post había tanteado por encima la siguiente idea:
Los números son operaciones y toman valor como operaciones. Sé lo que vale 3 cuando sé que representa ciertas operaciones posibles. Por ejemplo al definir la siguiente operación: 4 - 1 = 3 = 2+1, queda claro y sin duda alguna que 3 es un valor una unidad menor que 4, y una unidad mayor que 2.
Son las operaciones, pues, que determinan el valor y la magnitud, el orden y la naturaleza de lo que llamamos números. De hecho, cabría pensar que los números no son más que una operación.
Preguntarse: ¿qué número sigue de forma inmediata al número 3? Es una pregunta sin sentido, a no ser que establezcamos una operación que la defina de forma precisa y clara, como hemos hecho arriba al decir que el 4 sigue de forma inmediata a 3, al tener la acción "inmediata" aquí mismo definida mediante la noción de unidad. Si no está definida una operación de orden no hay forma de saber cuál es el número que sigue a 3 de forma inmediata. Tan siquiera pensarlo ya resulta, de hecho, completamente absurdo.
Es cierto que siempre podemos introducir nuevas operaciones y redefinir este "inmediato" considerando que entre 4 y 3 habrán otros números. De hecho, potencialmente podríamos definir que habría una infinidad al estipular que podríamos sacar tantos como quisiéramos. Pero para pensar eso hay que generar una operación para definirlo, acaso una operación de límite, y sólo a través de ella tomaría sentido lo que decimos.
Axiomas para determinar los números naturales como operaciones
Impulsado por la curiosidad despertada al jugar con estas ideas, raras, selectas y profundamente filosóficas, estos días he perdido un poco el tiempo desarrollando algunos axiomas para fundamentar la aritmética. Son axiomas algo distintos a los famosos de Peano (
ver aquí), que parten de la idea de que ya preexiste un número natural llamado "
unidad de los naturales". Pero Peano no definen las propiedades de este primer número natural llamado "
unidad de los naturales". Se limita a decir que es un número natural (y vete a saber qué significa eso) y que no es sucesor de ningún otro número natural:
Dado que esta "unidad de los naturales" no está casi definida en Peano, entonces no queda claro si estamos hablando del 1 o el 0; además de presentar otras muchas oscuridades. Los axiomas de Peano saben rudimentarios. Sin embargo, vale destacar como este sistema axiomático ha sido usado por los lógico-matemáticos durante 150 años como pilar sobre el que justificar gran parte de sus trabajos de axiomatización matemática. Sí, lo rudimentario es siempre fácilmente manejable si funciona un poco, pues no es muy complicado.
Dicho esto me sabe preciso añadir algo más. El intento de axiomatizar la aritmética viene ya de muy lejos: en el Parménides Platón presenta una axiomatización de la aritmética empleando un lenguaje "filosófico" como ejemplo, precisamente, de la importancia de axiomatizar el conocimiento para acceder a la certeza. En efecto, la axiomatización matemática ha sido una gran contribución platónica; al menos así se aprecia en el trabajo que nos ha llegado de su discípulo Euclides.
Esquema sobre el Parménides de Platón sobre las hipótesis de lo Uno
Todo seguido, cuelgo una axiomatización muy sui géneris basada en la idea de que un número natural es una operación muy concreta, además de básica, y de como a partir de ella se desarrollan las demás operaciones que llamamos números -
hasta las raíces. Ver axiomatización
aquí.
Lo más simple es siempre lo más difícil de definir.
Aquí termino el post, dejando una idea que servirá para empezar otro día: no es fácil definir qué es un número natural y cómo de tal definición, luego, se puede lograr definir gran parte de la matemática como un juego de operaciones. Y no es fácil porque para definir los números naturales es preciso definir, antes, "qué es la unidad natural", lo común a todos los naturales y por tanto, a lo que todos ellos pueden ser reducidos.
Y así mismo sucede también en geometría. Lo más difícil de definir ha sido el punto, hermano gemelo de la unidad y del número para los matemáticos durante los últimos siglos. Y la forma que tenemos ahora de definirlo es empleando aún un grado importante de indefinición. Por tal motivo, he empezado a esbozar unos axiomas geométricos para definirlo de otra manera, pero ya veremos...