Ya he hablado otras veces de este teorema en el blog de forma algo tangencial. Hoy quiero añadir algunos aspectos más al respecto, en especial, para que no se me olviden. Y para seguir dedicándolo a Chaitín, cuyo libro he vuelto a hojear estos días.
Los teoremas de Gödel surgen de un entorno racionalista: del deseo por desarrollar el pensamiento máquina -conocido también como pensamiento formal.
El pensamiento máquina quizás sea el pensamiento que distingue a la modernidad, en la medida que se rigió por el lema: -La realidad es una máquina perfecta, puesto que todo cuanto existe tiene una razón precisa de ser-
"Todas las múltiples ciencias y artes modernas no son más que filosofía aplicada"
Quizás fuera Leibniz quien mejor lo ilustró con su "principio de razón suficiente". Pero tal pensamiento, de un modo u otro, fue la luz que guio a los padres de la modernidad ya desde Descartes, o incluso desde Ramon Llull.
Defender que "todo tiene una razón de ser", como ya más tarde supo exponer de forma brillante Schopenhauer en su famoso trabajo "sobre la cuádruple raíz del principio de razón suficiente", implica presuponer 4 ideas filosóficas principales:
a) Todo fenómeno físico tiene una causa. Si una madera se enciende se debe a una causa, pues no lo hace espontáneamente y sin más. El comportamiento físico del cosmos está completamente determinado por una cadena causal cuyo fundamento último es autoevidente, al no tener causa alguna.
b) Todo fenómeno psíquico y toda acción humana obedece a un motivo. Si alguien odia a una persona será por algún motivo. El comportamiento humano está completamente determinado y en última instancia emerge de un fundamento psicológico primigenio y autoevidente (acaso la felicidad o el deseo o la libertad o la supervivencia).
c) Toda verdad lógica-matemática parte de una premisa. Una afirmación lógica o matemática es cierta cuando se deriva, o deduce, de una premisa cierta previa, dado que las verdades lógico-matemáticas no son ciertas porqué sí y sin fundamento. Todo desarrollo lógico-matemático está completamente determinado a ser el que es y emerge de un fundamento lógico primigenio autoevidente.
d) El fenómeno intuitivo como "causa" de las verdades inmediatas del ser -la metafísica. Los fundamentos físicos, psicológicos y lógico-matemáticos son especiales, por autoevidentes. Y sólo se puede acceder a lo autoevidente por intuición directa.
-------------------------------------------------------------
Bajo este resumen vemos, pues, como para la modernidad conocer "algo" implicaba conocer su razón de ser ¡Ir hasta sus orígenes y fundamentos primeros! Puesto que se presuponía y se esperaba que todo tuviese un origen y una raíz fundacional ¡Y que además fuera inteligible! *Aquí "ser inteligible" significa, simplemente, que se pueda explicar/comprender sin caer en una contradicción.
Precisamente, a este "ir hasta el origen de las cosas" se presentaba al público como un "hallar su demostración". Así por ejemplo, conocer qué es el fuego consistía en conocer sus causas y con ellas en mente se "demostraba" su comportamiento físico.
En definitiva: conocer el porqué y la razón de ser de un fenómeno, ya físico, psíquico-ético o lógico-matemático, implicaba, para una mentalidad moderna, demostrar su "verdadera realidad y forma de ser"; hecho que llevaba a esos pensadores a poder confiar ciegamente en tal conocimiento sin temer que cambiase o se alterase o pudiese ser criticado, puesto en duda y refutado.
Las raíces de la lógica-matemática
Como cualquier otro conocimiento también las matemáticas se articulan, siempre, sobre afirmaciones, enunciados, proposiciones, es decir, definiciones. Por ejemplo "2+2 = 5" es una proposición sobre la aritmética que define, a bote pronto, que "dos más dos son cinco".
En principio, hoy en día, entendemos que las afirmaciones, o definiciones, son siempre puras hipótesis, es decir, sentencias que pueden ser ciertas o falsas; aunque a veces aparecen algunas que si son ciertas, entonces han de ser falsas, y si son falsas entonces han de ser ciertas a la vez (enunciados contradictorios y por ello ininteligibles); y otras veces aparecen afirmaciones tautológicas y redundantes incapaces de ser jamás refutadas de modo que, al menos desde Parménides, se toman como autoevidencias y por eso, verdades inquebrantables, eternas y definitivas ¡Verdades en sí!
Ahora bien, desde que somos niños la proposición "2 + 2 = 5" es juzgada siempre, y sin dudas, como falsa, mientras entendemos que lo correcto sería que "2+2=4" o bien, que "2+2+1=5", sin la necesidad de comprender y cuestionarse qué es una tautología, una hipótesis o una contradicción. Sin embargo, la cuestión que plantearon los sabios modernos, quienes sí se inquietaban por dichas cuestiones difíciles y singulares, fue sumamente sutil y quisquillosa:
¿Y cómo fiarnos realmente de que esa primera proposición sea, sin duda, falsa, mientras que las dos siguientes sean siempre ciertas?
Descartes despacha este tema "muy a la francesa". Después de "demostrar" la existencia de Dios, como un ser infinito, perfecto, omnipotente, eterno, omnisciente y bueno -de modo que jamás nos engañaría-, deduce de ello que si una afirmación nos parece clara y evidente, entonces por bondad divina ya será indudablemente cierta -¡Y, "au revoir"!-
En dicho caso, dado que "2+2=5" parece en seguida falso, a mí y a cualquiera, entonces, semejante enunciado estaría, siempre, definitivamente refutado para el francés. En cambio, dado que "2+2=4" y "2+2+1=5" parecen manifiestamente ciertos para cualquiera que sepa contar, entonces lo serán sin duda siempre.
Descartes, pues, apelaba con suma inocencia a una facultad intuitiva-metafísica felizmente superficial para verificar las afirmaciones: simplemente si nos parecen claras y evidentes ya están demostradas y serán ciertas siempre.
Sin embargo, a Leibniz le ponía sumamente nervioso esta afrancesada y feliz superficialidad intuitiva de Descartes; su riguroso espíritu parecía necesitar ir hasta la raíz del porqué "2+2= 5" es falso y, en cambio, "2+2 = 4" es cierto. Y el alemán pensó que gracias a los principios de no contradicción y de razón suficiente podía esclarecer mucho mejor tan sutil misterio, y decir más cosas al respecto.
Leibniz desarrolló con esmero germánico ambos principios hasta llegar a la idea de Dios como la causa de todas las causas, y también de sí mismo. Y bajo semejante definición consideró lícito establecer "el principio de identidad" como fundamento primero de toda veracidad: lo que es causa de sí mismo es cierto por sí mismo, de modo que se puede tomar como una verdad elemental, primera, tautológica, es decir, analítica o autoevidente.
En tal sentido, para Leibniz la definición, "2+2=4", es verdad porque se demuestra a sí misma: la primera parte "2+2" verifica inmediatamente la segunda "4", ¡y viceversa!, dado que cada una de las dos partes es causa necesaria y lógica de la otra ¡No puede ser de otra forma! De modo que, según interpreta el genio alemán, la proposición se está demostrando a sí misma ¡Es autoevidente!
"¿No fue Leibniz quién llamó a las verdades de la aritmética "juicios analíticos" y los tomó como verdades de razón?" Mi memoria.
En cambio, en "2+2=5" la proposición se contradice a sí misma, entiende el alemán, dado que si damos per verdadera la primera parte "2+2" ello implica, necesariamente, que la segunda, "5", sea falsa; y viceversa. Por consiguiente, el genio alemán justificaba que se juzgase tal afirmación aritmética como indudablemente falsa por que sus partes se contradicen y por tanto, obtenemos una proposición imposible e inimaginable ¡Por impensable!
"Es cierto y posible todo cuanto se puede pensar y falso, imposible e inexistente lo que no se puede pensar" Dicho defendido por todos los lógicos y metafísicos desde Parménides.
Pero Leibniz nos cuenta algo más. Una vez verificado que "2+2=4" es cierto, entonces sería posible desarrollar inmediatamente y por deducción una nueva verdad aritmética, acaso "2+2+2 = 4+2= 6", y así seguir de forma indefinida, pasando a demostrar con ello todos los infinitos números pares existentes.
Vale reconocer que tan imponente racionalismo de Leibniz divagaba clarísimamente ya de forma implícita en el feliz y superficial pensamiento de Descartes, también en Spinoza y tantos otros, pero es en el alemán donde la idea toma cuerpo de forma ya bastante precisa, depurada y técnica, ejerciendo una influencia magistral y poderosa en el pensamiento moderno europeo.
No hay duda, históricamente hablando, de que la vieja Europa quedó hipnotizada durante siglos por los sacrosantos y metafísicos principios "de razón suficiente" y "de no contradicción", con los cuales se deriva el "principio de identidad", o de "autoevidencia"; siendo la idea de Dios, o del Ser, el paradigma de ella como fundamento de todo lo posible, real y existente.
Y es con este principio de autoevidencia con el cual el pensamiento moderno se atrevió, sumamente ilusionado -vale señalar, por cierto-, a proclamar por todos los vientos que cualquier certeza debe proceder, y por ello demostrarse en última instancia, a partir de una verdad fundamental primera autoevidente, analítica, tautológica ¿¡Divina!? Una verdad que se demuestra a sí misma, porque se comprende a partir de sí misma sin requerir de nada más.
El mundo metafísico fue ese mundo-delirio de las cosas en sí, de las ideas en sí, de las formas en sí, de las verdades en sí, de las autoevidencias eternas, inmaculadas y divinas. Esas semillas omnipotentes capaces de hacer emerger de su seno el frondoso árbol de la existencia.
Hoy en día, que nos hemos vuelto mucho más mundanos y terrenales; que hemos perdido esa vieja ilusión y necesidad espiritual, dogmática y metafísica, por suspender, como si fuesen estrellas solitarias, un puñado de verdades puras y divinas en medio de la oscura y sideral "Nada" que supuestamente rodea la Existencia, hemos cambiado el gusto y el criterio: cuando saboreamos estas sublimes y vacías autoevidencias redundantes que regurgitan los lógicos al cimentar toda su arquitectura de verdades y demostraciones no vemos más que hipótesis perpetuas y nubes incoloras: afirmaciones que, si bien nunca vamos a poder refutar, tampoco las podremos tomar jamás como verdaderas. Sí, vemos el espectáculo de la lógica ya con otros ojos; y, sobre todo, otro humor.
Un juego de niños
Vale reconocer que contra esta postura racionalista y metafísica que estaban tejiendo los más imponentes sabios modernos se podría levantar cualquier niño de 5 años mostrando que si afirmamos la certeza de "2+2=4" se debe, sencillamente, a nuestra experiencia: basta con coger dos cosas, juntarlas con dos cosas más para apreciar que tenemos 4 cosas ¡Es un mero contar! -¿Hay que darle tantas vueltas?- Cabría preguntarse al apreciar estos esperpénticos vuelos de la razón hasta alcanzar las nubes, reino de lo divino, que nos proponen los sabios.
Kant respondería que sí, que resulta crucial cuestionárselo para profundizar en los misterios del conocimiento humano. Y puesto en ello llegó a la conclusión de que la aritmética procedería, en efecto, de la experiencia; quizás de una experiencia harto rudimentaria, como sería el contar con los dedos de la mano cuando somos pequeños o nos falta potencia mental, pero una vez gozamos de ella procedería de la capacidad de visualizar mentalmente los números como objetos abstractos, para luego contarlos intuitivamente.
Ahora bien, el alemán también añade que éste contar de cabeza no es suficiente para fundamentar la aritmética, porque no sirve para asegurar que las verdades visualizadas, o intuidas, sean verdades universales y necesarias; es decir, lo sean siempre ¡Además de la experiencia se requiere de una razón para que dote la intuición de una ley necesaria y universal!
Para Kant sólo la intuición, o experiencia, nos permite descubrir la verdad, pero ésta no puede asegurar que tal verdad sea universal y necesaria. Es la razón, con su poder de comprensión, quien lo puede asegurar.
Curiosamente, basta con observar que a un niño de cinco años le preguntas -¿"2+2"?- Y después de contar te contesta "4", pero dado que él no entiende que este resultado es necesario y universal cuando se lo vuelves a preguntar vuelve a contar con los dedos de nuevo ¡Como si pudiese esperar que ahora se diese un resultado distinto! ¿O acaso lo hará por otros motivos?
En todo caso, Kant defendía la necesidad de que las verdades aritméticas tengan una doble raíz o causa: una de empírico-intuitiva y otra de lógica -de necesaria y universal. Con motivo las consideró "juicios sintéticos a priori". Y con ello negaba que las verdades de la aritmética fueran una mera tautología, una simple verificación dogmática, directa y autoevidente, como establecía Leibniz, dado que ello implicaría, por ejemplo, que la factorización de cualquier número podría ser, siempre, evidente e inmediata ¡Hecho que no es ni por asomo! Aunque Leibniz esgrimiría, posiblemente, que de algún modo oscuro y aún desconocido la factorización debería resolverse de forma inmediata solo con ver el número a factorizar, sin embargo nos falta inteligencia para comprenderlo: -Dios sí lo puede hacer- Susurraría el alemán.
El s.XIX, el siglo de los sistemas axiomáticos
¿Qué es un sistema axiomático?
Conceptualmente no es más que un simple código de normas y reglas, y como tal da órdenes, es decir, desarrolla afirmaciones, proposiciones, definiciones, exigencias, etc.
Para un código de normas, o de axiomas/premisas/reglas/criterios, sólo son correctas aquellas afirmaciones que se derivan directamente de él, es decir, que obedecen al código ¡Y acaso son causa de él! En cambio, se consideran incorrectas aquellas afirmaciones o exigencias que no obedecen, o no siguen, al código normativo.
En concreto, para los lógico-matemáticos, las proposiciones que obedecen a los axiomas de un sistema lógico concreto se juzgan como verdades, por estar "demostradas" por el sistema, es decir, por derivar de sus axiomas -o al menos por obedecerlos. En cambio las proposiciones que contradicen, niegan o se salen de lo que pautan los axiomas del sistema, entonces se juzgan como falsos, paradójicos (contradicen al sistema), erróneos, independientes o no demostrables.
Y en efecto, existen un disparidad de códigos axiomáticos en multitud de campos distintos: matemáticas, lógica, ética, política (las leyes), gestión y administración, física, computación, metafísica, etc. En fin, todo lo que sea regular, ordenar, clasificar, exigir, controlar, juzgar y valorar, construir, determinar, obligar, etc, requiere de un código de normas, reglas y criterios para pautar y seleccionar de entre todo lo posible, qué puede y no puede ser válido, bueno y correcto.
De modo que el estudio de los códigos normativos, como tales y más allá del ámbito donde se apliquen, resulta ser fundamental para el desarrollo humano. Y de aquí surgen dudas principales: ¿Acaso existe un código normativo que sea superior y más bueno, justo y potente que todos los demás posibles? ¿Qué requisitos y características debe mostrar un código normativo para ser funcional y ejercer un poder sobre la materia sobre la que actúa para darle un orden? ¿Cómo se desarrollan los códigos normativos y se relacionan entre ellos: se puede integrar uno a otro siempre sin problemas o generan vacíos, conflictos y contradicciones?
A partir del s.XIX el estudio de los códigos normativos pareció tomarse cada vez más en serio en multitud de campos, y en especial en el de la lógica-matemática.
Hallazgos axiomáticos del s.XIX
Todos los sabios modernos tenían sumamente asumido, gracias a los trabajos de Euclides, que la geometría era una ciencia axiomática, puesto que las verdades de la geometría tradicional se deducen y demuestran a raíz de los cinco postulados de Euclides. Estos postulados se habían considerado autoevidentes durante siglos; nadie dudaba de ellos y se tomaban por sacrosantos -Basta con leer a Descartes como emplea uno de ellos como indicio de verdades indudables por claras y distintas.
Sin embargo, a partir de Gauss se pone ya en duda el quinto postulado; el de las paralelas. Y para finales del s.XIX ya se tiene claro que el quinto postulado no es autoevidente ni necesario, sino más bien contingente, por así decirlo: si se toma este postulado como cierto se genera un tipo de verdades geométricas (las euclidianas) y si se toma como falso se generan otras verdades geométricas diferentes (las no euclidianas) ¡De repente aparecen en escena todo un abanico de geometrías dispares!
Estos hallazgos pusieron de manifiesto la importancia capital de axiomatizar todas las verdades que se conocían para hallar las demás verdades que se sospechaban que existían, tomando los axiomas como la causa y la raíz de cualquier verdad matemática, y/o científica. A fin de cuentas se observaba como escogiendo un sistema de axiomas u otro era posible generar unas "verdades u otras".
Cabe destacar en este contexto la aparición de los primeros axiomas lógicos de la aritmética por parte de Peano a finales del s.XIX. Se trata de un sistema axiomático basado en la teoría de conjuntos, desarrollada por los primeros lógico-matemáticos (Frege, Cantor, Russell, etc) como un intento para demostrar, de algún modo, lo que ya había defendido Platón: que todas las matemáticas se fundamentarían en ideas puras autoevidentes, es decir, en principios inteligibles estrictamente formales -principio de no contradicción, de razón suficiente, de identidad, de tercio excluido, de comparación, etc-; y no en intuiciones empírico-corporales, es decir, metáforas, ficciones y analogías; como bien propuso ya Nietzsche por primera vez, tomó a su manera Poincaré o recientemente desarrollan Lakoff, Nuñez, y otros tanto.
Vale destacar, precisamente, como esta axiomatización de Peano, que tiene un papel principal en esta historia que vamos contando, es formalmente incompleta con lo cual por más axiomas que se le añadan, siempre le faltarán para poder demostrar afirmaciones sobre la aritmética; además de no dejar muy clara la definición de unidad.
Y cabe decir algo más: ni de lejos el de Peano es el único sistema axiomático para la aritmética; las viejas reglas de sumar, restar, multiplicar y dividir y con las que aprendemos a operar desde niños son, de hecho, ya una axiomatización efectiva de la aritmética. Ahora bien, los axiomas de Peano son los que más gustan a los lógico-matemáticos, porque les parece que dejan entrever su fundamento formal al proceder de la teoría de conjuntos.
Con todo, cabe observar el poder de la axiomatización. Más allá de que esta sea formal (lógica) o no lo sea. La axiomatización es un "crear el juego al que vamos a jugar", decidiendo qué es posible y qué no, y de qué manera puede ser posible. Otra cosa es que el juego generado por una cierta axiomática nos guste, nos sea útil y efectiva o le sepamos sacar más o menos jugo. Pero la axiomática nos permite generar realidades a porrones, como ya entendió Wittgenstein al final de su vida.
De hecho, más allá de la aritmética que hemos aprendido de pequeños es posible generar otras aritméticas distintas simplemente manipulando los axiomas, reglas y criterios aritméticos; ahí tenemos como ejemplo la aritmética modular o la lunar. Un ejemplo de operaciones en aritmética lunar:
En fin, entre finales del s.XIX y principios del XX el fervor con que se trató el tema de la axiomatización fue creciendo, en especial entre esos lógicos insuflados de algún modo por el espíritu idealista germánico, quienes vieron en la axiomática formal una nueva vía para alcanzar la autoevidencia, la demostración pura, la verdad absoluta y definitiva ¡El mundo metafísico de los objetos en sí! Un mundo axiomático etéreo y divino capaz de sintetizar a todos los demás en su seno y por tanto, capaz de actuar como la máquina de Dios: la que siempre dice la verdad y nunca nada se calla .
El sueño moderno: la ilustración y su máquina de la verdad
La edad moderna tomó cuerpo con la ilustración, y esta soñó con que todos los múltiples y variados aspectos humanos, a primera vista tan diferentes y dispares, en última instancia deben de emerger de una misma y única ley universal autoevidente que sintetice en su seno a todas las demás.
Bajo tal sueño se desveló una esperanza: poder deducir, o demostrar, todas las verdades del mundo a partir de un único sistema axiomático considerado una especie de Oráculo capaz de explicarlo todo y revelar, de tal guisa, el misterio de la existencia.
Quizás deberíamos tomar a Frege como punto de partida, aunque seguramente deberíamos recordar a Leibniz, Kant, Fichte o Hegel como padres espirituales de este movimiento característicamente germánico. Ahora bien, sí, fue Frege quién intentó aplicar dicho espíritu filosófico en el ámbito de la lógica-matemática, fundando la famosa filosofía analítica, y que tantos devotos ha tenido a lo largo del s.XX, y aún hoy en día.
El primer lenguaje formal: la lógica proposicional
Frege se leyó a Kant, criticó su noción de "juicio analítico" y que tomara las verdades de la aritmética como "juicios sintéticos a priori". Para el alemán los enunciados aritméticos serían analíticos, como esgrimía Leibniz, de modo que se deberían de derivar unos de otros de forma inmediata y automática ¡Deberían tener un fundamento lógico y autoevidente!
Sin embargo le fascinó la idea de un mundo conceptual completamente formal, vacío e inaprensible: una realidad trascendente repleta de objetos y facultades universales y necesarias puramente deducibles a partir de sus funciones y el modo de articularse entre sí.
No me cabe mucha duda de que, con Kant, se vio la posibilidad de coger el lenguaje cotidiano, destilarlo hasta dejarlo seco sin sabor alguno al sacarle todo cuanto contiene de semántica sensual, de carnaza, intuición y vivencia ¡Dejando sólo su forma conceptual!
Con tan radical proceso de purificación lingüística Frege creó un primer lenguaje -un sistema de axiomas- articulado sobre símbolos vacíos que se relacionan entre ellos a través de órdenes o funciones, la cuales se toman como necesarias y universales. Es la lógica proposicional -Más tarde empezó a desarrollar otro lenguaje formal más expresivo, y hoy tenemos ya unos cuantos diferentes.
En este primer lenguaje formal, muy básico, tenemos símbolos o letras, como p,q,r,s,t, u, x...; representan una afirmación o proposición simple cualquiera, dado que carecen de significado propio. Es decir, cada proposición simple puede adquirir una infinidad de significados intuitivos variopintos y diferentes ¡Son puras variables!
El valor de estas variables o proposiciones simples, pues, no es semántico, sino que se le da un valor de verificación, y como tal o puede ser verdadera o falsa.
Luego hay diferentes órdenes (funciones) que se toman como necesarias y universales, es decir, como siempre iguales: ahí tenemos la conjunción, la disyunción, la negación, la implicación, etc.
Y es entonces cuando diferentes proposiciones simples se relacionan, conectan o articulan empleando esas órdenes lógicas a fin de generar proposiciones cada vez más complejas. Obtenemos, pues, cada vez fórmulas proposicionales más expresivas. Por ejemplo:
Proposición simple 1: p
Proposición simple 2: q
Orden: conjunción; exige que una proposición se una a la otra
Proposición compleja: "p conjunción q "; que se lee como: dado p se une a q.
Puesto que tanto p como q carecen de significado intrínseco no es posible valorar si son ciertas o falsas semánticamente, es decir, juzgando su significado natural, sino que sólo se pueden juzgar como ciertas o falsas según sus relaciones lógicas: según la forma como se articulan. Y con motivo llamamos a estos lenguajes "formales".
Diría que fue Wittgenstein quién desarrolló precisamente las famosas tablas de verdad para estos lenguajes formales -su Tractatus lógico philosophicus fue, en gran medida, una poetización de este proyecto formalista que se estaban creando bajo el sueño de hallar un oráculo que nos contara, sin duda alguna, qué es el mundo.
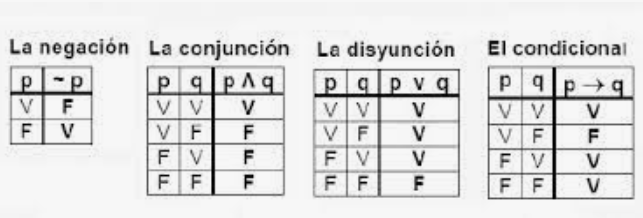
Así pues, en este nuevo lenguaje, árido e insípido como un cristal empañado, cada proposición deviene una especie de fórmula lógica con una única y exclusiva tabla de verdad. La tabla de verdad de nuestro ejemplo es la que pone "la conjunción" en la siguiente imagen:
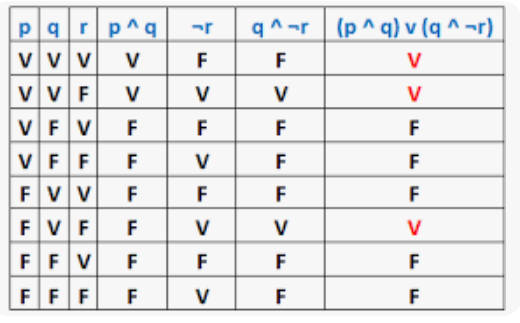
Obsérvese como las tablas de verdad dan todas las combinaciones posibles de "verdad y falso" que puede manifestar una proposición lógica según sea el valor de verdad/falso de sus componentes más simples. Obviamente, cuanto más compleja sea una proposición, mayor será su tabla de verdad, cuyos ítems crecen exponencialmente con su complejidad:
Cabe destacar dos cosas principales de este primer lenguaje formal ideado por Frege:
1) Estamos ante un lenguaje capaz de juzgar cuando una afirmación es cierta o falsa de forma automática, mecánica, ciega, sin reflexionar ni sentir nada, es decir, aplicando una serie de pasos finitos y preestablecidos al dedillo. A este procedimiento mecánico se le llama "el circuito lógico" de la proposición y cuyo valor y significado viene dictaminado, exclusivamente, por su tabla de verdad.
2) Este circuito lógico con el que podemos determinar de forma mecánica y "ciega" todas las posibilidades de verdad o falsedad de una proposición resulta ser, curiosamente, homeomorfo con los circuitos eléctricos. En otras palabras, a partir de un circuito lógico se puede construir un circuito eléctrico completamente equivalente; basta convertir todos los valores "verdad" por 1 y los valores "falso" por 0 en la tabla de verdad. Y el 1 significa "interruptor abierto" -no pasa electricidad; mientras 0 significa "interruptor cerrado" -sí pasa electricidad por el circuito.
De repente, esos primeros lógicos se dieron cuenta que habían desarrollado un tipo de lenguaje árido e insípido como una placa de metal, con lo cual, lejos de ser un estorbo, abría una nueva oportunidad: permitía hablarle precisamente a una máquina eléctrica ¡Era posible dar ordenes, funciones e instrucciones a un aparato mediante el diseño de un circuito eléctrico específico!
Aparece la idea de generar un procesador o computadora: un circuito eléctrico capaz de obedecer un algoritmo; de modo que nos resulta posible emplear el circuito para alcanzar un resultado concreto y, con ello, resolver problemas de forma automática.
Empieza, pues, la era de la computación y la inteligencia artificial.
Formalizando las matemáticas
Cuando Russell descubrió lo que estaba creando el lobo solitario de Frege en su laboratorio de destilaciones lingüísticas alucinó. Enseguida entendió la singularidad de ese sistema axiomático formal y completamente automatizable: parecía posible soñar de algún modo con usar dicho lenguaje para analizar sistemáticamente todas las combinaciones de verdad/falso posibles de una afirmación en cualquier tipo lenguaje: des del lenguaje hablado cuotidiano, al matemático, al físico, etc.
En efecto, dada una afirmación en lenguaje ordinario cualquiera, por ejemplo, "si mañana sale el sol, entonces me iré a la playa", era posible traducirla a la lógica proposicional; acaso mediante dos variables o proposiciones simples (p,q) y una función (de condición o implicación). Pongamos un ejemplo:
Variable 1: p = mañana sale el sol
Variable 2: q = mañana iré a la playa
Función: implicación = si ... entonces ...
Fórmula proposicional: p implica q = si mañana sale el sol, entonces me iré a la playa.
Cada proposición simple p,q sólo puede ser formalmente o cierta o falsa. Por tanto, siempre tiene dos estados posibles de "veracidad".
La tabla de verdad siguiente nos dice cuando la proposición informal "si mañana sale el sol, entonces, iré a la playa" es formalmente cierta o falsa según sean ciertas o falsas sus proposiciones simples (p,q). Veámoslo:
Apreciamos, pues, que la afirmación "si mañana sale el sol, entonces me iré a la playa" será formalmente siempre verdad excepto cuando "mañana sale el sol"(p) sea verdad, pero "mañana me iré a la playa"(q) sea falso; es decir: sólo será falsa en el caso de que mañana no me vaya la playa aunque saliera el sol. En todos los demás casos siempre será verdad.
Sin embargo recibió una carta de un jovencísimo Bertrand Russell, aún estudiante de filosofía en Cambridge, quien había estado leyendo su trabajo con suma atención a raíz de sus críticas hacia el trabajo preliminar de Peano, y que llevó al italiano a corregirlo. El inglés le comunicaba estar completamente de acuerdo con su enfoque formalista, pero que había encontrado una paradoja oculta en la teoría de conjuntos -La famosa paradoja del barbero.
Esta paradoja tumba sin compasión la teoría de conjuntos elaborada hasta el momento por el propio Frege y Cantor. ¿Qué significaba esto? Pues que su procedimiento de análisis formal no había sido capaz de detectar tamaño error "oculto" en la teoría de conjuntos ¡Algo fallaba en su trabajo de verificación y análisis de errores! Son dignas de recordar las palabras que soltó el propio Frege después de leer la carta que le envió Russell:
"Difícilmente puede haber algo más indeseable para un científico que ver el derrumbe de sus cimientos justamente cuando la obra está acabada. La carta del Sr. Bertrand Russell me ha puesto en esta situación...”.
Ahora bien, también es cierto que tanto Russell como Frege pensaban que este fallo se podría solventar en algún momento; que era un dolor de cabeza circunstancial.
En 1912 Russell y Whitehead publicaban su famosísimo "Principia mathematica", aportando destacadas innovaciones sobre la teoría de conjuntos y el análisis formal, pero sin solventar ese problema de forma clara, y sobre todo, sin lograr hallar aún el fundamento formal de la aritmética.
Diez años más tarde, en 1921, Wittgenstein sacaba su "Tractatus logico philosophicus", en el cual se presenta y avanza la existencia de un lenguaje formal único como metafísica última del mundo, y su razón de ser. De hecho, ya se aprecia allí como se aventura a pregonar que estaríamos ante un lenguaje coherente y completo, y, como tal, capaz de "decir todo lo que se puede decir sin ambigüedades". Ahora bien, dado que Wittgenstein lo consideraba el lenguaje oracular, madre de todo el conocimiento posible, parece fantasear con tal idea al afirmar: "sobre lo que no se puede hablar se debe callar". 30 años más tarde, pero, reconocerá que "lo que no se puede decir en un lenguaje se puede decir en otro".
¿Qué es un sistema axiomático formal?
En el wikipedia lo explican bastante bien:
Las 3 partes principales de un sistema formal:
-Un lenguaje formal: un conjunto de símbolos y "reglas gramaticales" que permiten construir afirmaciones formales, o fórmulas lógicas, que el sistema es capaz de "leer", comprender, y por consiguiente, analizar. Cada sistema formal suele tener un lenguaje propio; los números de Gödel serían un ejemplo. Para la lógica proposicional tenemos por simbologia las letras del abaecedario para designar variables (p,q,r,s,t...) y símbolos lógicos para designar funciones, órdenes o nexos necesarios.
-Un conjunto de axiomas: los axiomas son afirmaciones formales necesaria y universalmente verdaderas para el sistema y gracias a las cuales éste demuestra si una afirmación analizada es verdadera o falsa. Muchas veces se suelen considerar autoevidentes.
-Reglas de inferencia: son los criterios de transformación, interpretación o traducción que emplea el sistema a fin de analizar las fórmulas lógicas que le son dadas. El sistema recibe una fórmula y mediante sus reglas de inferencia, junto con sus axiomas, la interpreta y traduce a una conclusión o respuesta determinada.
Nota: cualquier circuito lógico que emplee un sistema formal en el análisis de fórmulas se articula sobre sus axiomas y sus reglas de inferencias. Por tanto, cualquier algoritmo que se aplique sobre un circuito lógico debe obedecerlos.
Propiedades del sistema: Finitista, completitud, consistencia y decidibilidad
A finales de la década de los veinte y después del trabajo de gente como Lowenheim, Hilbert o el joven Gödel, ya estaban establecidas las primeras propiedades que pueden presentar los sistemas formales.
La primera, a grosso modo, es que deben ser finitistas, es decir, todos los análisis que realizan dichos sistemas sobre afirmaciones dadas deben regirse mediante algoritmos -procedimientos mecánicos finitos claros y evidentes a partir de sus axiomas y reglas de inferencia establecidas, capaces de resolver problemas concretos.
En este sentido, como ya se ha dicho varias veces, la idea consistió en hallar un Oráculo: un sistema formal capaz de traducir al dedillo toda afirmación del mundo posible a su lenguaje formal, para luego analizarla mediante un algoritmo omnisciente a fin de demostrar cuales son verdaderas y cuales falsas.
Y se sabe qué propiedades debería tener un Oráculo: debería ser un sistema axiomático completo(1) y consistente(2) , al ser capaz de probar algorítmicamente si cualquier afirmación analizada es verdadera o falsa de forma coherente.
(1) Un sistema axiomático es completo cuando está formado por un conjunto finito de axiomas y no precisa de ninguno más para probar si un enunciado formal es verdadero o falso. Lo enunciados probados como verdaderos pasan a llamarse "teoremas" del sistema.
(2) Un sistema axiomático es consistente cuando es imposible que el sistema demuestre como verdadera una afirmación y, luego, también demuestre como verdadera a su contraria. Es decir, cuando el sistema nunca puede generar teoremas contradictorios entre sí.
Por otro lado, a la dicha capacidad que tienen los sistemas formales completos de decidir si una afirmación formal cualquiera que analiza es verdadera o falsa se la llama decidibilidad. Y por consiguiente, toda afirmación formal que pueda ser analizada por un sistema axiomático completo será decidible.
Entendido esto, si empleamos un sistema incompleto para analizar afirmaciones formales siempre encontraremos afirmaciones indecidibles: el sistema se ve incapaz de probar algorítmicamente si son verdaderas o falsas ¡Si son o no son teoremas! Y se queda colgado.
Estas fórmulas lógicas indecidibles se toman como "independientes" del sistema. Y la única forma para que no dejen al sistema colgado es postulándolas como nuevos axiomas del sistema ¡Integrándolas! Hecho siempre posible si el sistema, con ello, no se vuelve inconsistente y empieza a determinar teoremas a lo loco.
Por tanto, todo cuanto no puede ser probado ya como verdadero ya como falso por el sistema debería de pasar a formar parte del propio sistema con la idea que este amplíe su capacidad expresiva y pueda ya "decir más cosas". Sin embargo, no pocas veces al intentar completar un sistema indecidible, éste se vuelve entonces inconsistente y empieza a demostrar "teoremas" contradictorios.
Puede darse el caso, pues, que un sistema se vuelva inconsistente al ser decidible, o bien se vuelva indecidible al ser consistente. ¿Será porqué su análisis es ciego?
Presentación de los teoremas de incompletitud de Gödel
En 1929 un jovencísimo Gödel demostró que la lógica de primer grado, algo más explicativa que la lógica proposicional antes expuesta con un ejemplo sencillo, es un sistema decidible. Ante este primer logro Gödel quiso atacar ya directo al dilema que desde Frege había mantenido soñando a los logicistas y que Hilbert, ante el fracaso continuo, había vuelto a recordar en 1930: ¿será posible traducir todas las afirmaciones de la aritmética a esa lógica, demostrar con ello sus fundamentos formales y poder ya empezar a usarla como el preludio de lo que sería la gran máquina de la verdad?
Para tantear tal posibilidad Gödel diseñó un artilugio simbólico harto complejo, abstracto y fascinante, a partir de una serie de características específicas que debe cumplir el aparato.
La función principal de semejante armatoste conceptual consistía, primero, en traducir la aritmética de Peano a la lógica de primer grado con el fin de formalizar las afirmaciones aritméticas y dejarlas listas para que el "monstruo" las triture y analice.
Por así decirlo, las afirmaciones sobre la aritmética como "9 es un número primo sí y sólo sí es divisible por 5" o "2+2=4" o bien, "si tengo un número par cualquiera entonces es divisible por 2" eran traducidas a símbolos y expresiones lógicas de primer grado. Con ello obteníamos ya fórmulas listas para ser analizadas por esa filigrana de artilugio, esperando, demostrar si son verdad o falsas.
Pero esto no es todo -la máquina precisaba hacer algo más. Gödel ideó un mecanismo por el cual el sistema fuera capaz de identificar sus propios enunciados formales, y que, luego, podía analizar. Para ello el genio lógico se inventó un lenguaje de codificación: sus famosos números de Gödel.
Los números de Gödel son, siempre, números naturales que se construyen de la siguiente manera: se adjudica un número natural específico, y muy bien pensado por Gödel, a cada símbolo de la lógica de primer grado, y luego se aplica una operación para cada enunciado formal con el fin de adjudicarle un número de Gödel característico según sean sus símbolos.
De manera que aquí el juguete lingüístico de Gödel aplicaba una segunda traducción: toda afirmación ya formalizada de la aritmética ahora pasaba a codificarse como un número de Gödel específico e irrepetible, gracias al cual el sistema lo podía identificar sin error y ambigüedad, puesto que cualquier número de Gödel podía volverse a descodificar automáticamente en su enunciado formal original. En la wikipedia se explica medianamente bien este proceso de traducción o codificación con un ejemplo:
¿Qué construye pues Gödel? Un aparato de traducción sumamente simbólico que por un lado tiene números de Gödel, que son siempre números naturales característicos, y por el otro tiene enunciados formales que hablan sobre la aritmética ¡Y hay siempre una relación biyectiva entre números de Gödel y enunciados formales! Pues cada número de Gödel identifica a un y sólo un enunciado formal sobre la aritmética
Observamos, pues, como el genio de Gödel crea un sistema formal autorreferente al ser capaz de analizarse y tomar consciencia de sí mismo ¡Pues este juguete es capaz de hablar sobre sí mismo!
Y sin embargo, al llegar aquí, el artilugio empezó a tartamudear, echar humó y petó.
Y aparece la incompletitud
Gödel descubrió que cuando el sistema ideado tiene que "tomar consciencia de sí mismo", peta ¡Y lo hace fuerte! Quizás al sistema le falte hipocresía... o sinvergüenza para saltarse a la torera la contradicción que le sobreviene.
Parece ser que el sistema se encuentra con una especie de contradicción de algún modo bastante similar a la "paradoja del barbero" ya presentada antes, descubierta por Russell (o Zermelo) en teoría de conjuntos; y que Groucho Marx se atrevió a ilustrar de forma hilarante, cuando soltó: "Caballeros, nunca pertenecería a un club que admitiera como socio a alguien como yo".
En su versión original la paradoja de Russell, o del barbero, decía: "el conjunto de todos los conjuntos que no pertenecen a sí mismos no puede ni pertenecer a sí mismo ni no pertenecer a sí mismo".
En este caso, la paradoja en el ámbito de la formalización de la aritmética parece surgir cuando llevamos el juguete de Gödel más o menos por el siguiente sendero de afirmaciones, al considerar "x" una afirmación cualquiera sobre la aritmética:
1) El aparato nos permite afirmar sin problemas que, "las afirmaciones aritméticas que afirman x se pueden probar verdaderas". A este enunciado le corresponde un número de Gödel como identificador, acaso el número GN1. Y para esta afirmación el aparato nos demuestra que es verdadera.
2) El aparato también nos permite negar lo contrario que lo anterior, y por tanto decir "ninguna afirmación aritmética que afirme no-x se puede probar verdadera". Y a este enunciado le corresponde su propio número de Gödel, acaso GN2. Y para esta afirmación el aparato también nos demuestra que es verdadera.
3) Pero entonces el aparato nos permite afirmar, "ninguna afirmación aritmética que afirme GN2 se puede probar verdadera", es decir, que "ninguna afirmación aritmética que afirme "ninguna afirmación aritmética que afirme no-x se puede probar verdadera" se puede probar verdadera". Y resulta, entonces, que el invento explota. *De hecho, esta larga y autorrecurrente afirmación se puede resumir en "ninguna afirmación que afirme una verdad se puede probar verdadera". Una expresión que no es más que una nueva forma de presentar la paradoja del mentiroso, que dice: "esta afirmación es falsa".
Apreciamos, aquí, que si el aparato toma este último enunciado por falso, entonces, paradójicamente, demuestra que lo que dice la propia afirmación es verdadero (que la afirmación es falsa).
Y si ante lo razonado antes el aparato toma por verdadera la afirmación, entonces, entra directamente en contradicción con lo que afirma la propia afirmación, demostrando que es falsa ¡Menudo embrollo!
De hecho, lo que hace Gödel una vez demostrado que el sistema nos da afirmaciones como "esta frase es falsa", es demostrar que el aparato, al ser autorreferente, también puede crear una frase del tipo "el sistema es consistente"; y con ambas presentar la siguiente afirmación: ""si el sistema es consistente" implica que "esta frase es falsa", mientras demuestra que tal frase es cierta y por tanto, se considera un teorema del sistema. De hecho, estamos propiamente ante la formulación correcta del primer teorema de incompletitud de Gödel.
La cuestión, ahora, es analizar qué "circunstancias" lógicas son necesarias para que la frase ""el sistema es consistente" implica que "esta frase es falsa" sea un teorema, como bien demuestra Gödel.
Para entenderlo fácil, basta con hacer un poco de trampas manipulativas mediante un pequeño análisis proposicional tomando (p,q) como variables:
p = el sistema es consistente
q = esta frase es falsa
Función: implicación = si... entonces...
si p entonces q = si el sistema es consistente entonces "esta frase es falsa"
Aplicamos la tabla de la verdad de la implicación:
Resumiendo vemos que la frase "si el sistema es consistente entonces "esta frases es falsa"" es verdadera en dos situaciones posibles; :1) Cuando "el sistema es consistente" es siempre cierta y "esta frase es falsa" o es cierta o es falsa (opción 1y2)
2) Cuando "el sistema es consistente" siempre es falsa y "esta frase es falsa" o es cierta o es falsa. (opciones 3y4)
Sin embargo, sabemos que si p es cierta, entonces q es indecidible y por tanto no se puede afirmar ni si es cierta ni falsa. De modo, que la primera sitación (opción 1y2) queda relegada. Sólo nos queda la segunda opción: que el sistema sea inconsistente y demuestre por un lado que "esta frase es falsa" como verdadera y luego, por otro lado, también, demuestre lo contrario: que es falsa.
De modo que lo que nos viene a decir el segundo teorema de incompletitud es que al demostrarse que "el sistema es consistente entonces "esta frases es falsa"" es un teorema (es cierta), ello significa que la premisa "el sistema es consistente" es falsa (no es ningún teorema del sistema). En la wikipedia parecen resumirlo así:
Breve comentario
Se ha escrito bastante sobre lo que significarían semejantes resultados de incompletitud; incluso se ha dicho que quien dice haberlo entendido, entonces no lo ha entendido.
Después de pensar un poco con ello me aventuraré a dar una opinión:
Lo que nos cuentan ambos teoremas es que dado un sistema formal con unas características determinadas, como bien cumple la aritmética de Peano al traducirla a lógica de primer grado, es que, si éste es consistente, entonces generará una afirmación del tipo "esta frase es falsa", poniendo de manifiesto que el sistema es incompleto y por tanto, que existen afirmaciones que le resultarán independientes. Ahora bien, si intentamos axiomatizar tales afirmaciones, entonces, ello vuelve al sistema incoherente.
En resumen, que para ciertos sistemas formales resulta inevitable que siendo estos consistentes sean indecidibles, hecho que implica que sean inconsistentes.
Esta situación no es nueva en la historia del lenguaje. Me atrevería a decir que los viejos sofistas griegos ya tantearon estas paradojas de forma simple e informal, al menos si atendemos a Platón. No en vano Gödel parece interpretar sus propios resultados desde una óptica más bien platónica al ver allí, de algún modo, una solución. Y no es el único; Penrose también lo hace.
Imagino que la influencia de Schopenhauer sobre Gödel en estos temas fuera destacada; a fin de cuentas, el alemán tomó públicamente de Platón el defender unos límites del entendimiento racional humano, más allá de los cuales se contraría la verdad.
Platón y los límites del lenguaje
Una de los aspectos cruciales de Platón es su relación entre lenguaje, pensamiento y verdad. Para el griego, la verdad prexiste como ideas o formas en sí; y sólo se accede mediante el pensamiento puro, la intuición: un tipo de experiencia anímica excepcional y divina, que nos sobreviene por reminiscencia.
Entonces, este pensamiento divino puede transformarse en lenguaje o expresión comunicativa mediante un proceso de materialización, por así decirlo. Por tanto, el lenguaje sería una vulgarización y un proceso de deterioro del pensamiento, que transforma la experiencia pura de la idea en algo más y más tosco, confuso, limitado e imperfecto: el símbolo, el concepto, la normativa que regula el encadenamiento de símbolos, etc para que expresen, de algún modo, tan sublime experiencia de la idea.
En este sentido, para el griego el lenguaje, y dentro de él su forma suprema, la argumentación o dialéctica (la mecanización de argumentos), no sirven para alcanzar la verdad, en todo caso sirven para despertar y empezar a buscarla. Pero para alcanzar lo verdadero es preciso de algo no lingüístico tan ligero y etéreo que nos permita, ya no andar paso a paso como pretendían los finitistas, sino echar la mente a volar hasta las alturas. Es necesaria la intuición.
Parece que esta fue la interpretación que sacó Gödel de sus estudios. Y que era pareja a la de Schopenhauer, que se sobreentiende leyendo lo que se ha comentado de él al principio del post. En efecto, Gödel parece hacer esto:
1) Presupone la existencia de verdades metafísicas; autoevidencias.
2) Entiende que sus teoremas marcan los límites del lenguaje formal o pensamiento mecanizado empleando algoritmos -límites de la argumentación y la lógica.
c) Más allá de estos límites lingüísticos, y también empíricos por supuesto, se ocultan las grandes verdades metafísicas, que como semillas, permitirían que florezcan los nuevos conocimientos.
d) Sólo mediante intuición pura nuestra consciencia puede acceder a ellas y verse preñada de su luz, hecho que nunca sucederá mediante el mero razonamiento, la demostración o el cálculo.
De hecho, Gödel sacó una breve demostración ontológica, que normalmente se vende como una demostración de Dios, pero que en el fondo es, sobre todo, un intento de demostrar la existencia de un "reino de las evidencias o verdades en sí", las cuales constituirían "lo real". Sí, Gödel es un metafísico de tomo y lomo, y lo que hace aquí es metafísica: poetiza sobre la existencia de una realidad en sí -lo que no hace es teología.
En la demostración el lógico nos dice: Existen las verdades autoevidentes, sobre las cuales se articula la realidad toda. Con razón actúan como propiedades positivas o esenciales de las cosas: pues una cosa existe como algo real en virtud de sus propiedades esenciales, es decir, su verdades autoevidentes. Una de estas propiedades, por ejemplo, es "la existencia". Y estas propiedades existen porque las ha creado Dios. Y Dios existe porque existen tales verdades autoevidentes que hacen posible lo real. En conclusión, existen verdades autoevidentes, o propiedades esenciales, siendo necesariamente Dios su génesis, porque el mundo real-verdadero existe.
Sin embargo, no podemos acceder a tal mundo ni mediante demostración formal ni experiencia corporal, sino que de forma sibilina se apela a una hipotética intuición pura o metafísica.
El problema es que, como ya destacó Nietzsche, este mundo real-verdadero de las verdades en sí, soñado por todos los lógico-metafísicos, no existe, sino como mentira, suposición y sueño ¡Nada más!. Pero excepto Nietzsche, en los últimos 150 años prácticamente nadie más se ha dado cuenta de la comedia que aquí se ha representado -pondría a Chaitín como excepción-: que las autoevidencias, las tautologías, las verdades en sí, no son más que eternas hipótesis; puro humo ¡Y ese es precisamente su poder!
Sin embargo, al creer en la existencia de un mundo real-verdadero se creyó, en este caso, que las verdades matemáticas preexisten como objetos etéreos que esperan ser descubiertos, y que los teoremas de Gödel más bien demostrarían que los razonamientos lógicos, y formales, son insuficientes para alcanzarlos a todos ¡Y descubrir ya como es ese mundo real-verdadero al completo! Gödel lo cuenta así de forma resumida:
Este punto es compartido por otros pensadores, acaso Penrose, quien expuso de forma larga y pormenorizada su postura al respecto en "la nueva mente del emperador".
Penrose expone que ni nuestra mente es, simplemente, una máquina de pensar ni tampoco resulta posible simularla mediante una máquina de pensar, es decir, una computadora o una IA. Y extrapola esta idea al universo entero en base a los teoremas de Bell, que indican la no computabilidad del sistema cuántico.
¿Y qué significa esto? Penrose destaca la imposibilidad de reducir la existencia a un sistema lógico que mediante un único algoritmo sea capaz de reproducir/demostrar todas las "verdades" del mundo real, que suponemos que existe más allá del mundo confuso que vivimos, mientras le daría sustento y entidad.
Y esto es cierto, por lo que sabemos. Sin embargo, la cuestión es ¿Y por qué es imposible? ¿Por qué aparecen los teoremas de incompletitud al intentar crear un Oráculo?
Esto es lo que Chaitín se preguntó desde joven, y con su duda encontró una respuesta fascinante: las matemáticas no tienen un fundamento lógico, formal y completamente determinado, como los idealistas habían soñado desde hace siglos. Si hay un fundamento sobre el cual estructurar las matemáticas éste será, más bien, el azar.
Y además, Chaitin parece congeniar en gran medida con la postura de Nietzsche, Poincaré, Lakoff sobre la construcción y génesis de los conceptos matemáticos: su naturaleza metafórica, ficticia, creativa.
Conclusión
Los teoremas de incompletitud han sido extensamente comentados durante décadas, y siempre dándole vueltas desde una perspectiva metafísica, idealista, en fin, presuponiendo que la verdad existe de por sí, es dada a priori y que la inteligencia humana puede descubrir y entender. Sólo he leído a Chaitin revalorizando estos prejuicios antiquísimos. Y más sorprendente aún: después de sus trabajos, aún así, escucho continuar un monótono silencio respecto a lo que plantea Chaitín. Me parece digno de estudio psicológico de nuestra época.









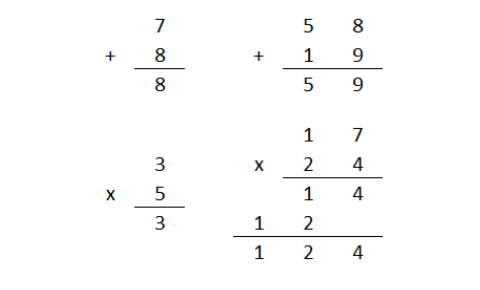














No hay comentarios:
Publicar un comentario